16.
Konstruisati ikosaedar, obuhvatiti ga sferom, kao i ranije navedena tela, i dokazati da je ivica ikosaedra iracionalna i to takozvana ``manja''.
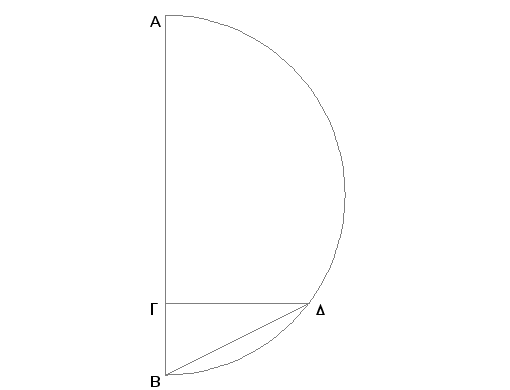
Odmerimo AB kao prečnik date sfere i podelimo ga tačkom G tako da AG bude četiri puta veće od GB. Dalje, nacrtajmo na DB polukrug ADB, povucimo iz G normalu GD na AB, nacrtajmo DB, i konstruišimo krug EZHQK poluprečnika DB. Pa upišimo u krug EZHQK jednakostrani i jednakougli petougao EZHQK, prepolovimo lukove EZ, ZH, HQ, QK, KE tačkama L, M, N, X, O i nacrtajmo LM, MN, NX, XO, OL, EO. Biće tada LMNXO jednakostran i jednakougli petougao i EO strana desetougla. I kroz tačke E, Z, H, Q, K u ravni kruga povucimo normale Ep, ZP, HS, QT, KU jednake poluprečniku kruga EZHQK, i spojimo pP, PS, ST, TU, Up, pL, LP, PM, MS, SN, NT, TX, XU, UO, Op. I pošto je svaka od Ep i KU normalna na istoj ravni, biće Ep paralelno sa KU [XI.6]. A one su i jednake. Ali prave koje spajaju sa iste strane krajeve jednakih i paralelnih duži jednake su i paralelne [I.33]. Prema tome su prave pU i EK jednake i paralelne. No EK je strana jednakostranog petougla. Pa znači da je i pU strana jednakostranog petougla upisanog u krug EZHQK. Iz istih razloga i svaka od duži pP, PS, ST, TU je strana jednakostranog petougla upisanog u krug EZHQK. Dakle petougao pPSTU je jednakostran. Pošto je pE strana šestougla, a EO - desetougla i ugao pEO je prav, biće pO strana petougla, jer je kvadrat strane petougla jednak zbiru kvadrata strane šestougla i strane desetougla upisanih u isti krug [XIII.10]. Iz istih razloga i OU je strana petougla. Takođe i pU je strana petougla. Prema tome je trougao pOU jednakostran. Iz istih razloga i svaki od trouglova pLP, PMS, SNT, TXU je jednakostran.
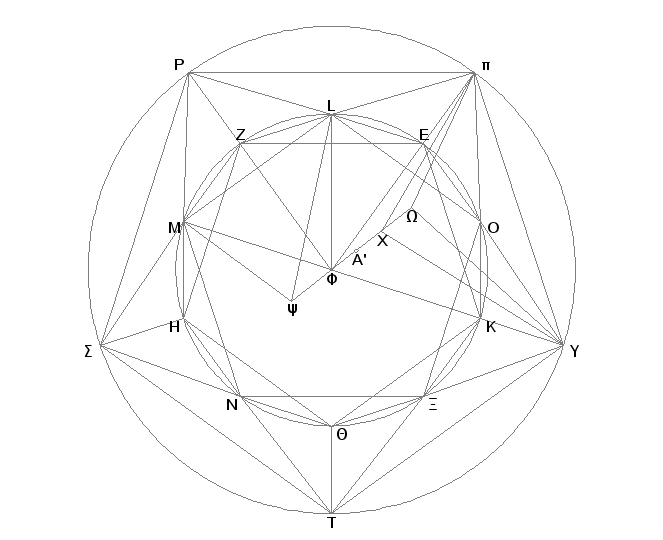
I pošto je dokazano da je svaka od duži EL i pO strana petougla, a takođe i LO strana petougla, biće i trougao pLO jednakostran. Iz istih razloga i svaki od trouglova LPN, MSN, NTX, XUO je jednakostran. Uzmimo za centar kruga EZHQK tačku F. Iz tačke F spustimo normalu FW na ravan kruga i produžimo kao FY na drugu stranu. Pa odmerimo stranu šestougla FX i svaku FY, XW kao strane desetougla i spojimo pW, pX, UW, EF, LF, LY, YM. I pošto je svaka od FX i pE normala na ravni kruga, onda su FX i pE paralelne [XI.6], a one su i jednake. Znači, i EF i pX su jednake i paralelne [I.33]. No EF je strana šestougla, te prema tome i pX je strana šestougla. I pošto je pX strana šestougla, XW strana desetougla i ugao pXW prav, biće pW strana petougla [XIII.10]. Iz istih razloga i UW je strana petougla, jer, ako povučemo FK i XU, oni su jednaki i suprotnog položaja; a kako je FK, kao poluprečnik, strana šestougla, biće i XU strana šestougla [IV.15, Posledica]. No XY je strana desetougla i ugao UXW je prav, znači i UW je strana petougla [XIII.10]; a i pU je strana petougla. Prema tome je i trougao pUW jednakostran. Iz istih razloga i svaki od preostalih trouglova sa osnovicama pP, PS, ST, TU i sa vrhom u tački W je jednakostran. Zatim, pošto je FL strana šestougla, a FY desetougla i ugao LFY prav, biće LY strana petougla [XIII.10]. Iz istih razloga, ako uzmemo duž MF, koja je strana šestougla, biće i MY strana petougla. No i LM je strana petougla. Prema tome je trougao LMY jednakostran. Na sličan način se dokazuje da je i svaki od preostalih trouglova sa osnovicama MN, NX, XO, OL i vrhom u tački Y jednakostran. Na ovaj način je konstruisan ikosaedar obuhvaćen sa dvadeset jednakostranih trouglova.
Treba ga obuhvatiti datom sferom i dokazati da je ivica ikosaedra iracionalna i to takozvana ``manja''.
Zaista, pošto je FX strana šestougla, a XW - desetougla, FW je podeljeno tačkom X neprekidno i veći deo je FX [XIII.9]; znači WF je prema FX kao FX prema XW. Ali FX je jednako FE, a XW jednako FY. Prema tome je WF prema FE kao FE prema FY. I uglovi WFE i EFY su pravi. Znači, ako uzmemo duž EW, biće i ugao YEW prav, zbog sličnosti trouglova YEW i FEW. Iz istih razloga, pošto je WF prema FX kao FX prema XW, a WF jednako YX i FX jednako Xp, biće YX prema Xp kao pX prema XW. Zatim, iz istih razloga ako uzmemo pY, biće ugao kod p prav [VI.8]. Prema tome polukrug konstruisan na YW proći će i kroz tačku p [III.31]. I ako se pri nepokretnom YW, polukrug obrne i ponovo vrati u početni položaj od kojeg je počeo obrtanje, on će proći kroz tačku p i kroz preostale tačke ikosaedra i biće ikosaedar obuhvaćen sferom. Tvrdim da je to data sfera. Zaista, prepolovimo FX tačkom A'. I pošto je duž FW podeljena tačkom X neprekidno i njen manji deo je WX, biće kvadrat na zbiru WX i polovine većeg dela XA' pet puta veći od kvadrata na polovini većeg dela [XIII.3]. Prema tome je kvadrat na WA' pet puta veći od kvadrata na A'X. No WY je dvaput veće od WA', a FX dvaput veće od A'X. Znači kvadrat na WY je pet puta veći od kvadrata na XF. I pošto je AG četiri puta veće od GB, biće AB pet puta veće od BG. No AB je prema BG kao kvadrat na AB prema kvadratu na BD [VI.8, V, Def. 9], pa prema tome je kvadrat na AB pet puta veći od kvadrata na BD. A dokazano je da je i kvadrat na WY pet puta veći od kvadrata na FX. I DB je jednako FX, jer je svaki od njih poluprečnik kruga EZHQK. Prema tome je i AB jednako YW. Ali AB je prečnik date sfere. Dakle, i YW je prečnik date sfere. Na ovaj način je ikosaedar obuhvaćen datom sferom.
Tvrdim da je ivica ikosaedra iracionalna, takozvana ``manja''. Zaista, pošto je prečnik sfere racionalan i kvadrat na njemu je pet puta veći od kvadrata na poluprečniku kruga EZHQK, biće i poluprečnik kruga EZHQK racionalan, dakle racionalan je i njegov prečnik. No ako se u krug sa racionalnim prečnikom upisuje jednakostran petougao, onda je strana petougla iracionalna, takozvana ``manja'' [XIII.11]. No strana petougla EZHQK je ivica ikosaedra. Na ovaj način je ivica ikosaedra iracionalna, takozvana ``manja''.