13.

Konstruisati piramidu, obuhvatiti je datom sferom, i dokazati da je kvadrat na prečniku sfere jedan i po puta veći od kvadrata na ivici piramide.

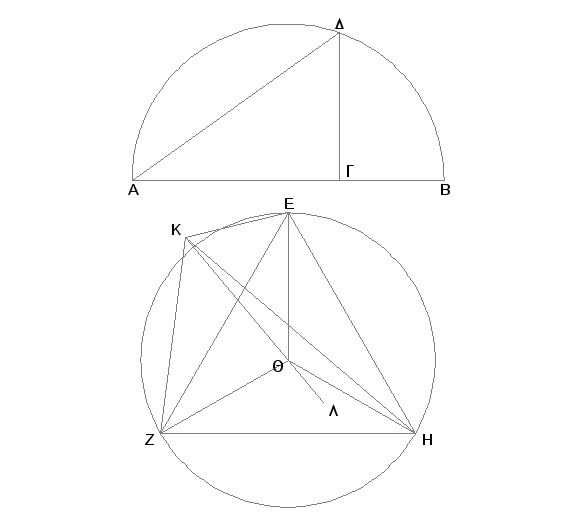
Odmerimo duž AB, jednaku prečniku date sfere, i presecimo je tako tačkom G da AG bude dvaput veće od GB. Nacrtajmo na AB polukrug ADB, konstruišimo kroz tačku G duž GD upravnu na AB i spojimo A i D pravom AD. Nacrtajmo krug EZH poluprečnika DG, upišimo u krug EZH jednakostran trougao EZH [IV.2], uzmimo za centar kruga tačku Q [III.1], i povucimo duži EQ, QZ i QH.FOOTNOTEU komentaru je navedena još jedna slika za ovu teoremu.} I iz tačke Q konstruišimo pravu QK normalnu na ravan kruga EZH [XI.12]. I odmerimo na QK duž QK jednaku AG. Povucimo KE, KZ, KH. I pošto je prava KQ normalna na ravni kruga EZH, ona obrazuje prave uglove sa svim pravama koje je seku i nalaze se u ravni kruga EZH [XI, Def. 3]. No seče je svaka od pravih QE, QZ, QH, pa prema tome je QK upravna na svakoj od QE, QZ, QH. I pošto je AG jednako QK, a GD jednako QE i obrazuju prav ugao, biće i osnovica DA jednaka osnovici KE [I.4]. Iz istih razloga i svako od KZ i KH jednako je DA. Prema tome su tri duži KE, KZ, i KH jednake među sobom. I pošto je AG dvaput veće od GB, biće AB triput veće od BG. No, kako ćemo to kasnije dokazati, AB je prema BG kao kvadrat na AD prema kvadratu na DG. Prema tome je kvadrat na AD triput veći od kvadrata na DG. I kvadrat na ZE je triput veći od kvadrata na EQ [XIII.12], a DG je jednako EQ. Dakle, i DA je jednako EZ. Ali, kako je dokazano, i svako od KE, KZ, KH jednako je DA, pa je znači, i svako od EZ, ZH, HE jednako svakom od KE, KZ, KH. Prema tome su četiri trougla EZH, KEZ, KZH i KEH jednakostrani. Na ovaj način je obrazovana piramida od četiri jednakostrana trougla, čija je osnova trougao EZH, a vrh tačka K.
Ali se traži da bude obuhvaćena datom sferom i da se dokaže da je jedan i po kvadrat na prečniku sfere jednak kvadratu na ivici piramide.
Zaista, produžimo u pravcu prave KQ pravu QL i odmerimo QL jednako GB. I pošto je AG prema GD kao GD prema GB [VI.8, Posledica], a AG je jednako KQ, i GD jednako QE i GB jednako QL, biće KQ prema QE kao EQ prema QL. I prema tome je pravougaonik obuhvaćen od KQ i QL jednak kvadratu na EQ [VI.17]. I svaki od uglova KQE i EQL prav. Znači polukrug konstruisan na KL, prolazi kroz E [VI.8, III.31] [pošto će, ako konstruišemo EL, ugao LEK biti prav, jer je trougao ELK sa istim uglovima kao i svaki od trouglova ELQ i EQK]. Ako se pri nepokretnom KL, polukrug pri obrtanju ponovo vrati u početni položaj od kojeg je počeo obrtanje, on će proći i kroz tačke Z i H, jer ako se povuče ZL i LH, uglovi kod Z i H će na sličan način biti pravi i piramida biti obuhvaćena datom sferom. Zaista, KL, poluprečnik ove sfere, jednak je prečniku AB date sfere, jer je KQ odmereno jednako AG i QL jednako GB.
Tvrdim takođe da je kvadrat na prečniku sfere jedan i po puta veći od kvadrata na ivici piramide.
Pošto je AG dvaput veće od GB, biće AB triput veće od BG, a posle zamene jednog dela drugim, biće BA jedan i po puta veće od AG. No BA je prema DG kao kvadrat na BA prema kvadratu AD [pošto će ako se povuče DB, BA biti prema AD kao DA prema AG, i to na osnovu sličnosti trouglova DAB i DAG i stoga što je prvo prema trećem kao kvadrat na prvom prema kvadratu na drugom]. Prema tome je kvadrat na BA dva i po puta veći od kvadrata na AD. A BA je prečnik date sfere i AD ivica piramide.
Na ovaj način je kvadrat na prečniku sfere jedan i po puta veći od kvadrata na ivici piramide. A to je trebalo dokazati.