Ako kod jednakostranog i jednakouglog petougla dve duži spajaju uglove preko jednog, one dele jedna drugu neprekidno i njihovi veći delovi jednaki su strani petougla.

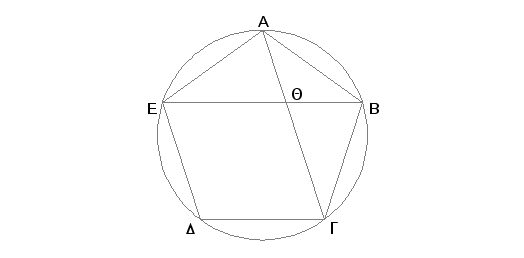
Neka u jednakostranom i jednakouglom petouglu ABGDE duži AG i BE, koje spajaju iz temena A i B uglove preko jednog, seku jedna drugu u tački Q. Tvrdim, da je svaka od njih podeljena tačkom Q neprekidno i da su njihovi veći delovi jednaki strani petougla.
Zaista, opišimo oko petougla ABGDE krug ABGDE [IV.14]. Pošto su dve duži EA i AB jednake dvema dužima AB i BG i one obuhvataju jednake uglove, biće i osnovica BE jednaka osnovici AG, trougao ABE jednak trouglu ABG, i preostali uglovi jednaki preostalim uglovima, svaki svakom, koji su obuhvaćeni jednakim stranama [I.4]. Prema tome je ugao BAG jednak uglu ABE. Znači, ugao AQE je udvostručeni ugao BAQ [I.32]. I ugao EAG je dvaput veći od ugla BAG, jer je luk EDG dvaput veći od luka GB [III.28, VI.33]. Prema tome je ugao QAE jednak uglu AQE. Znači, i duž QE jednaka je AE, tj. jednaka je i AB [I.6]. I pošto je duž BA jednaka duži AE, biće i ugao ABE jednak uglu AEB [I.5]. No dokazano je da je ugao ABE jednak uglu BAQ. Prema tome je i ugao BEA jednak uglu BAQ. I kod dva trougla ABE i ABQ ugao ABE je zajednički. Dakle, preostali ugao BAE jednak je preostalom uglu AQB [I.32]. Prema tome trouglovi ABE i ABQ imaju jednake uglove. I na taj način imamo proporciju: EB je prema BA kao AB prema BQ [VI.4]. No BA je jednako EQ, znači, BE je prema EQ kao EQ prema QB. No BE je veće od EQ, pa će i EQ biti veće od QB [V.14].
Na ovaj način BE je podeljeno tačkom Q neprekidno i veći deo QE je strana petougla. Slično se dokazuje da je i AG tačkom Q podeljeno neprekidno i da je GQ jednako strani petougla. A to je trebalo dokazati.