18.
Odrediti ivice pet proučenih tela i uporediti ih među sobom.
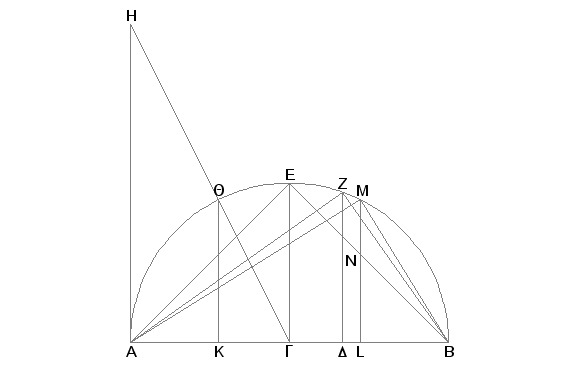
Uzmimo AB kao prečnik date sfere i tačkom G ga tako podelimo da AG bude jednako GB i tačkom D tako da AD bude dvaput veće od DB, pa na AB konstruišimo polukrug AEB, kroz G i D povucimo normale GE i DZ na AB i spojimo AZ, ZB, EB. Pošto je AD dvaput veće od DB, biće AB triput veće od BD. Ili, posle zamene jednog dela drugim, BA je jedan i po puta veće od AD. No BA je prema AD kao kvadrat na BA prema kvadratu na AZ [V, Def. 9, VI.8], jer trougao AZB ima iste uglove kao i trougao AZD. Prema tome je kvadrat na BA jedan i po puta veći od kvadrata na AZ. No i kvadrat na prečniku sfere je jedan i po puta veći od kvadrata na ivici piramide [XIII.13]. Kako je AB prečnik sfere, biće AZ jednako ivici piramide.
Zatim, pošto je AD dvaput veće od DB, biće AB triput veće od BD. No AB je prema BD kao kvadrat na AB prema kvadratu na BZ [V, Def. 9, VI.8]. I kvadrat na AB je triput veći od kvadrata na BZ. No i kvadrat na prečniku sfere je triput veći od kvadrata na ivici kocke [XIII.15]. A kako je AB prečnik sfere, biće BZ ivica kocke.
I pošto je AG jednako GB, biće AB dvaput veće od BG. No AB je prema BG kao kvadrat na AB prema kvadratu na BE. Prema tome je kvadrat na AB dvaput veći od kvadrata na BE. No i kvadrat na prečniku sfere je dvaput veći od ivice oktaedra [XIII.14]. A kako je AB prečnik dare sfere, biće BE ivica oktaedra.
Povucimo iz tačke A pravu AH upravnu na AB, odmerimo AH jednako AB i spojimo H sa G. Pa iz tačke Q povucimo normalu QK na pravu AB. I pošto je HA dvaput veće od AG, jer je HA jednako AB, a HA prema AG kao QK prema AB, biće i QK dvaput veće od KG. A kvadrat na QK je četiri puta veći od kvadrata na KG. I prema tome zbir kvadrata na QK i na KG, a to znači na QG, biće pet puta veći od kvadrata na HG. No QG je jednako GB, te prema tome je kvadrat na BG pet puta veći od kvadrata na GK. I pošto je AB dvaput veće od GB, a AD dvaput veće od DB, biće i ostatak BD dvaput veći od ostatka DG. Prema tome je BG triput veće od GD, a kvadrat na BG devet puta veći od kvadrata na GD. No kvadrat na BG je i pet puta veći od kvadrata na GK. Prema tome je kvadrat na GK pet puta veći od kvadrata na GD, dakle i GK je veće od GD. Odmerimo GL jednako GK, kroz L povucimo LM upravno na AB i spojimo MB. Pošto je kvadrat na BG pet puta veći od kvadrata na GK i AB je dvaput veće od BG, a KL je dvaput veće od GK, biće i kvadrat na AB pet puta veći od kvadrata na KL. No i kvadrat na prečniku sfere je pet puta veći od kvadrata na poluprečniku kruga pomoću kog se konstruiše ikosaedar [XIII.16, Posledica]. Kako je AB prečnik sfere, biće KL poluprečnik kruga pomoću kojeg se konstruiše ikosaedar. Prema tome je KL strana šestougla pomenutog kruga [IV.15, Posledica]. I pošto je prečnik sfere jednak zbiru strane šestougla i dve strane desetougla upisanih u pomenuti krug [XIII.16, Posledica], i AB je prečnik sfere, KL - strana šestougla i AK jednako LB, to je svaka od AK i LB strana desetougla upisanog u krug, pomoću kog se konstruiše ikosaedar. I pošto je LB strana desetougla, a ML - šestougla, jer je ML jednako duži KL, kao i duži QK, i to zbog toga što su podjednako udaljene od centra i što je svaka od QK i KL dvaput veća od KG. Prema tome je MB strana petougla [XIII.10]. Ali strana petougla je i ivica ikosaedra [XIII.16]. Na taj način MB je ivica ikosaedra.
I pošto je ZB ivica kocke, podelimo je tačkom N neprekidno i neka veći deo bude NB. Prema tome NB je ivica dodekaedra [XIII.17, Posledica]. I pošto je kvadrat na prečniku sfere jedan i po puta veći od kvadrata na AZ, ivici piramide, dvaput veći od kvadrata na BE, ivici oktaedra, triput veći od kvadrata na ZB, ivici kocke, onda od šest delova ( jedinica )kvadrata na prečniku sfere kvadrat na ivici piramide sadrži četiri, kvadrat na ivici oktaedra - tri i na ivici kocke dva dela. Prema tome je kvadrat na ivici piramide jedan i trećinu puta veći od kvadrata na ivici oktaedra, dvaput veći od kvadrata na ivici kocke, a kvadrat na ivici oktaedra je jedan i po puta veći od kvadrata na ivici kocke. Prema tome tvrdim, da se ivice tri pomenuta tela, - piramide, oktaedra i kocke, - nalaze među sobom u racionalnim razmerama. A ivice ostala dva, - ikosaedra i dodekaedra, - tvrdim, ne nalaze se, ni među sobom ni prema ranije navedenim, u racionalnim razmerama, jer su one iracionalne - ``manja'' [XIII.16] i apotoma [XIII.17].
Dokažimo sad da je ivica MB ikosaedra veća od ivice dodekaedra.
Zaista, pošto trougao ZDB ima iste uglove kao i trougao ZAB [VI.8], postoji proporcija: DB je prema BZ kao BZ prema BA [VI.4]. A kad su tri duži proporcijalne, biće prva prema trećoj kao kvadrat na prvoj prema kvadratu na drugoj [VI.20, Posledica, V, Def. 9]. Prema tome je DB prema BA kao kvadrat na DB prema kvadratu na BZ. I obrnuto: AB je prema BD kao kvadrat na ZB prema kvadratu na BD. Ali AB je triput veće od BD, pa je i kvadrat na ZB triput veći od kvadrata na BD. No kvadrat na AD je četiri puta veći od kvadrata na DB, jer je AD dva puta veće od DB. Prema tome je kvadrat na AD veći od kvadrata na ZB. Dakle, i AD je veće od ZB. Utoliko pre je i AL veće od ZB. I pri podeli AL u neprekidnoj razmeri, veći deo je KL, pošto je KL strana šestougla, a KA - desetougla [XIII.9]. A pri neprekidnoj podeli ZB veći deo je NB. Prema tome je KL veće od NB. No KL je jednako LM, znači i LM je veće od NB [a MB je veće od LM]. Prema tome utoliko pre je MB, ivica ikosaedra, veća od NB, ivice dodekaedra. A to je trebalo dokazati.
Tvrdim, da se sem pet pomenutih tela ne može konstruisati nijedno drugo telo, koje bi bilo obuhvaćeno jednakostranim i jednakouglim mnogouglovima.
Zaista, od dva trougla ili ma koje ravne slike rogalj se ne može sastaviti. Od tri trougla (se obrazuje) rogalj piramide, od četiri - oktaedra, od pet - ikosaedra. Od šest jednakostranih i jednakouglih trouglova sastavljenih kod jedne tačke rogalj se ne može obrazovati; zaista, pošto ugao jednakostranog trougla iznosi dve trećine pravog ugla, to je šest takvih uglova jednako četiri prava ugla, a to je nemoguće, jer je svaki rogalj obuhvaćen uglovima, čiji je zbir manji od četiri prava ugla [XI.21]. Iz istih razloga se ne može obrazovati rogalj ni sa više od šest takvih uglova u ravni. Sa tri kvadrata je obuhvaćen rogalj kocke. Sa četiri je nemoguće, jer se dobijaju ponovo četiri prava ugla. Od jednakostranih i jednakouglih petouglova se sa tri obrazuje dodekaedar. A od četiri je nemoguće, jer ugao jednakostranog petougla iznosi prav ugao i jednu petinu, pa prema tome su četiri ugla zajedno veći od četiri prava ugla, a to je nemoguće. Iz istih razloga se ne može obrazovati rogalj ni pomoću drugih mnogouglova.
Na ovaj način sem pet pomenutih tela ne može se konstruisati nijedno drugo telo koje bi bilo obuhvaćeno jednakostranim i jednakouglim mnogouglovima. A to je trebalo dokazati.