17.
Konstruisati dodekaedar, obuhvatiti ga sferom, kao i ranije navedena tela (figure), i dokazati da je ivica dodekaedra iracionalna, takozvana apotoma.
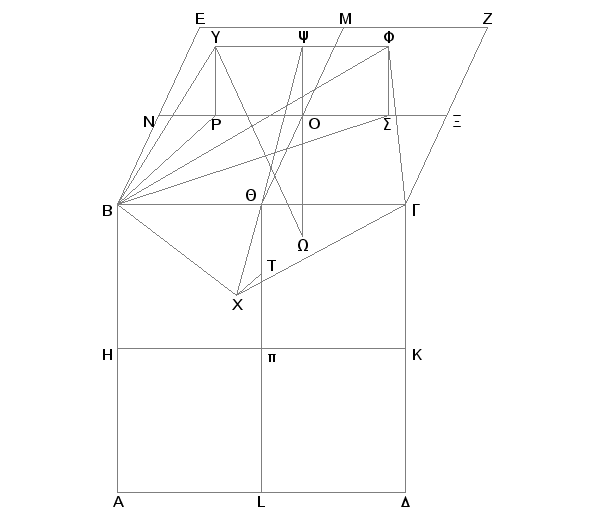
Uzmimo dve, jedna na drugoj upravne, ravni ABGD i GBEZ, ranije pomenute kocke. Svaku od ivica AB, BG, GD, DA, EZ, EB, ZG prepolovimo tačkama H, Q, K, L, M, N, X, spojimo HK, QL, MQ, NX, i podelimo svaku od NO, OX, Qp neprekidno tačkama P, S, T. I neka su PO, OS, Tp veći delovi. Pa iz tačaka P, S, T podignimo normale na ravnima kocke sa spoljašnje strane, odmerimo duži PU, SF, TX jednake dužima PO, OS, Tp i spojimo UB, BX, XG , GF, FU. Tvrdim da je UBXGF jednakostran ravan petougao i da ima jednake uglove. Zaista, uzmimo PB, SB i FB. Pošto je duž NO podeljena tačkom P neprekidno i veći deo je PO, biće zbir kvadrata na ON i NP triput veći od kvadrata na PO [XIII.4]. No ON je jednako NB i OP je jednako PU. Prema tome je zbir kvadrata na BN i na NP triput veći od kvadrata na PU. No zbir kvadrata na BN i na NP jednak je kvadratu na BP [I.47]. Znači kvadrat na BP je triput veći od kvadrata na PU. Tako da je zbir kvadrata na BP i na PU četiri puta veći od kvadrata na PU. No zbir kvadrata na BP i na PU jednak je kvadratu na BU. Prema tome je kvadrat na BU četiri puta veći od kvadrata na UP, dakle, BU je dvaput veće od PU. No i FG je dvapot veće od UP, pošto je SP dvaput veće od OP, tj. od PU. Na ovaj način BU je jednako UF. Slično se dokazuje, da je i svako od BX, XG, GF jednako svakom od BU i UF. Dakle, petougao BUFGX je jednakostran. Tvrdim da je i ravan. Zaista, povucimo kroz tačku O sa spoljašnje strane kocke pravu OY paralelnu svakoj od pravih PU i SF i povucimo YQ i QX. Tvrdim da je YQX prava. Zaista, pošto je duž Qp podeljena tačkom T neprekidno i veći njen deo je pT, biće Qp prema pT kao pT prema TQ. No Qp je jednako QO, a pT svakoj od TX i OY, dakle, QO je prema OY kao XT prema TQ. I duž QO je paralelna sa TX, pošto je svaka od njih normalna na ravni BD [XI.6]. I duž TQ je paralelna sa OY, jer je, zaista, svaka normalna na ravni BZ [XI.6]. No ako su dva trougla, YOQ i QTX, sa po dve proporcionalne strane, u takvom položaju da su dva kraka ugla jednog trougla paralelna sa homolognim kracima ugla drugog trougla, onda su njihove preostale strane u istoj pravoj [VI.32]. Prema tome su YQ i QX na istoj pravoj. No svaka prava je u istoj ravni [XI.1], pa je prema tome petougao UBXGF u jednoj ravni.
Tvrdim da on ima jednake uglove.
Zaista, pošto je duž NO podeljena tačkom P neprekidno i veći deo je OP [biće i zbir NO i OP prema ON kao ON prema OP], a OP je jednako OS [znači, SN je prema NO kao NO prema OS], prema tome, NS je podeljeno tačkom O neprekidno i veći deo je NO [XIII.5]. Znači, zbir kvadrata na NS i na SO je triput veći od kvadrata na NO [XIII.4]. No NO je jednako NB i OS je jednakom SF. Prema tome je zbir kvadrata na NS i na SF triput veći od kvadrata na NB. Tako da je zbir kvadrata na FS, SN i NB četiri puta veći od kvadrata na NB. No zbir kvadrata na SN i na NB jednak je kvadratu na SB. Na taj način zbir kvadrata na BS i na SF, a to je kvadrat na BF [jer je ugao FSB prav], četiri puta je veći od kvadrata na NB. Znači BF je dvaput veće od NB. Ali i BG je dvaput veće od BN. Prema tome je BF jednako BG. I pošto su dve strane BU i UF jednake dvema stranama BX i XG i osnovica BF jednaka osnovici BG, biće i ugao BUF jednak uglu BXG [I.8]. Slično se dokazuje da je i ugao UFG jednak uglu BXG. Prema tome su tri ugla BXG, BUF i UFG jednaka među sobom. Ali ako su kod jednakostranog petougla tri ugla jednaka među sobom, petougao ima jednake uglove [XIII.7]. Jednake uglove ima i petougao BUFGX. A dokazano je da je on i jednakostran. Na taj način petougao BUFGX je jednakostran i jednakougli i nalazi se na ivici BG kocke. Prema tome, ako na svakoj od dvanaest ivica kocke izvršimo isto, dobićemo prostornu figuru obuhvaćenu od dvanaest jednakostranih i jednakouglih petouglova, koja se zove dodekaedar.
Treba takođe i njega obuhvatiti datom sferom i dokazati, da je ivica dodekaedra iracionalna, takozvana apotoma.
Zaista, produžimo YO za YW. Prema tome se YO preseca sa dijagonalom kocke i polovi je, kako je to dokazano u pretposlednjoj teoremi jedanaeste knjige [XI.38]. Neka se one seku u tački W. Prema tome je W centar sfere koja obuhvata kocku i WO je polovina ivice kocke. Uzmimo UW. I pošto je duž NS podeljena tačkom O neprekidno i veći deo je NO, biće zbir kvadrata na NS i na SO triput veći od kvadrata na NO [XIII.4]. No NS jednako je YW, pošto je i NO jednako OW, a YO jednako OS. Ali je i OS jednako YU, pošto je jednako PO. Prema tome je zbir kvadrata na WY i na YU triput veći od kvadrata na NO. No zbir kvadrata na WY i na YU jednak je kvadratu na UW, znači i kvadrat na UW je triput veći od kvadrata na NO. Ali i kvadrat na poluprečniku sfere koja obuhvata kocku triput je veći od kvadrata na polovini ivice kocke, jer je ranije pokazano kako se konstruiše kocka i obuhvata sferom i kako se dokazuje da je kvadrat na prečniku sfere triput veći od kvadrata na ivici kocke [XIII.15]. No celo je prema celom kao i polovina (prvog) prema polovini (drugog). Ali NO je polovina kockine ivice, a UW je jednak poluprečniku sfere koja obuhvata kocku. I W je centar sfere koja obuhvata kocku. Prema tome je U tačka na sfernoj površini. Slično se dokazuje da se i svako od ostalih temena dodekaedra nalazi na sfernoj površini. Dodekaedar je prema tome obuhvaćen datom sferom.
Tvrdim da je ivica dodekaedra iracionalna, takozvana apotoma.
Zaista, pošto je duž NO podeljena neprekidno i veći deo je PO, a pri neprekidnoj podeli duži OX veći deo je OS, biće, pri neprekidnoj podeli cele duži NX, veći deo PS. Pošto je NO prema OP, kao OP prema PN, a u istoj su razmeri i udvostručeni, jer su delovi u istoj razmeri kao i multiplumi iste višestrukosti [V.15]. Prema tome je NX prema PS kao PS prema zbiru NP i SX. No veće je NX od PS. Zbog toga je i PS veće od zbira NP i SX. Na taj način je duž NX podeljena neprekidno i veći deo je PS. No PS je jednako UF, prema tome duž NX podeljena je neprekidno i ima veći deo UF. A pošto je prečnik sfere raciolnalan i kvadrat na njemu triput veći od kvadrata na kockinoj ivici, biće racionalna i duž NX, ivica kocke. No ako se racionalna duž deli neprekidno, svaki deo je iracionalan i to apotoma.
Na ovaj način je duž UF, ivica dodekaedra, iracionalna i to apotoma [XIII.6].