23.

Od tri ravna ugla, od kojih je zbir dva, proizvoljno uzeta, veći od preostalog, konstruisati rogalj. Pri tome treba da zbir ta tri ravna ugla bude manji od četiri prava ugla.

Neka su ABG, DEZ, HQK tri data ravna ugla od kojih je zbir dva, proizvoljno uzeta, veći od preostalog, a zbir tih uglova manji od četiri prava ugla. Treba od uglova ABG, DEZ, HQK konstruisati rogalj.
Odmerimo jednake duži AB, BG, DE, EZ, HQ, QK i spojimo AG, DZ, HK. Tada se može od duži jednakih AG, DZ i HK konstruisati trougao [XI.22]. Konstruišimo trougao LMN tako da AG bude jednako LM, DZ-MN i HK-NL i opišimo oko trougla LMN krug LMN; neka njegov centar bude X i spojimo LX, MX, NX. Tvrdim, da je AB veći od LX. Zaista, ako to nije tako, biće AB ili jednako LX ili manje od LX. Neka je, prvo, jednako. Tada će, pošto je AB jednako LX, AB jednako BG, a XL jednako XM, biti dve duži AB i BG jednake dvema dužima LX i XM, svaka svakoj. I osnovica AG je, po pretpostavci, jednaka osnovici LM. Prema tome je ugao ABG jednak uglu LXM [I.8]. Iz istih razloga je i ugao DEZ jednak uglu MXN, a i ugao HQK jednak uglu NXL. Na ovaj način su tri ugla ABG, DEZ i HQK jednaka sa tri ugla LXM, MXN i NXL. Ali zbir tri ugla LXM, MXN i NXL je jednak sa četiri prava ugla, znači i zbir tri ugla ABG, DEZ, HQK jednak je sa četiri prava ugla. S druge strane pretpostavljeno je da je taj zbir manji od četiri prava ugla. A to je besmisleno.

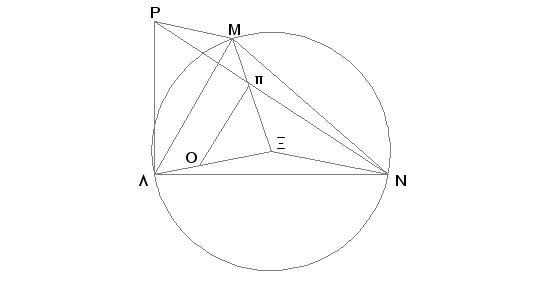
Dakle AB nije jednako LX. Tvrdim da AB neće biti ni manje od LX. Ako je to moguće, neka bude. Odmerimo XO jednako AB, Xp jednako BG i povucimo Op. Pošto je AB jednako BG, biće i XO jednako Xp. I ostatak LO jednak je pM. Prema tome je LM paralelna sa Op [VI.2] i trougao LMX je istih uglova sa trouglom OpX [I.29]. Znači XL se odnosi prema LM kao XO prema Op [VI.4], a posle permutovanja LX je prema XO kao LM prema Op [V.16]. No LX je veće od XO, pa prema tome je i LM veće od Op. Ali LM je odmereno jednako AG, pa je zbog toga i AG veće od Op. Pošto su sada dve duži AB i BG jednake dvema dužima QX i Xp, a osnovica AG je veća od osnovice Op, biće ugao ABG veći od ugla OXp [I.25]. Slično se dokazuje da je i ugao DEZ veći od ugla MXN, kao i ugao HQK od ugla NXL. Na taj način je zbir od tri ugla ABG, DEZ i HQK veći od zbira tri ugla LXM, MXN, NXL. Međutim je, po pretpostavci, zbir uglova ABG, DEZ, HQK, manji od četiri prava ugla. Stoga je zbir uglova LXM, MXN, NXL, utoliko pre, manji od četiri prava ugla. No on je i jednak. A to je besmisleno. Prema tome AB nije manje od LX. A dokazano je da nije ni jednako. Na taj način je AB veće od LX. Postavimo u tački X normalu Xp na ravan kruga LMN i neka kvadrat na XP bude jednak razlici kvadrata na AB i na LX. Pa spojimo PL, PM, PN. Pošto je PX normala na ravni kruga LMN, biće svaka od LX, MX, NX upravna na PX. I pošto je LX jednako XM, a XP zajednička strana spram pravog ugla, biće osnovica PL jednaka osnovici PM [I.4]. Iz istih razloga je i PN jednako svakoj od PL i PM. Prema tome su tri duži PL, PM, PN jednake među sobom. I pošto je, po pretpostavci, kvadrat na PX jednak razlici kvadrata na AB i LX, biće kvadrat na AB zbir kvadrata na LX i XP. Ali zbir kvadrata na LX i XP je jednak kvadratu na LP, pošto je ugao AXP prav [I.47]. Znači kvadrat na AB jednak je kvadratu na PL, a prema tome je AB jednako PL. No duž AB jednaka je svakoj od duži BG, DE, EZ, HQ, QK, a PL jednaka svakoj od PM i PN. Prema tome je svaka od duži AB, BG, DE, EZ, HQ i QK jednaka svakoj od PL, PM, PN. I pošto su dve duži LP i PM jednake dvema dužima AB i BG, a osnovica LM jednaka osnovici AG po pretpostavci, biće ugao LPM jednak uglu ABG [I.8]. Iz istih razloga je i ugao MPN jednak uglu DEZ, a ugao LPN uglu HQK.
Na ovaj način, od tri ravna ugla LPM, MPN, LPN, koji su jednaki datim uglovima ABG, DEZ, HQK, konstruisan je kod tačke P rogalj, čiji su ravni uglovi LPM, MPN, LPN. A to je trebalo izvesti.