10.

Nacrtati ravnokraki trougao, čiji je svaki ugao na osnovici dvaput veći od trećeg ugla.

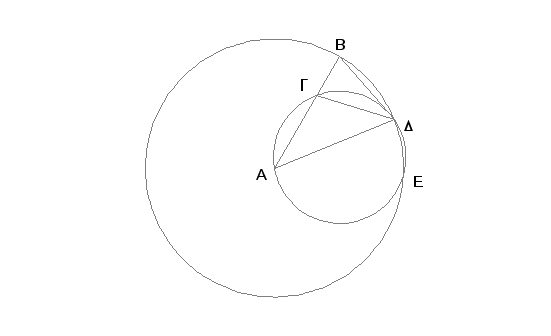
Odmerimo neku pravu AB i podelimo je tačkom G tako da pravougaonik obuhvaćen od AB i BG bude jednak kvadratu na AG [II.11]. I nacrtajmo krug BDE sa centrom u A a sa rastojanjem AB, pa upišimo u krug BDE pravu BD jednaku pravoj AG, koja nije veća od prečnika kruga BDE [IV.1]. Spojimo AD i DG, i oko trougla AGD opišimo krug AGD [IV.5].
Kako je pravougaonik od AB i BG jednak kvadratu na AG, a AG je jednako BD, biće pravougaonik od AB i BG jednak kvadratu na BD. A kako je van kruga AGD uzeta tačka B, i iz tačke B ka krugu AGD su povučene dve prave BA i BD jedna od njih seče krug, a druga dopire do njega, i pri tome je pravougaonik od AB i BG jednak kvadratu na BD, onda prava BD dodirivaće krug AGD [III.37]. Kako je sad prava BD tangenta i kroz tačku dodira D je povučena prava DG, biće ugao BDG jednak uglu DAG upisanom u suprotni otsečak kruga [III.32]. Kako je sad ugao BDG jednak uglu DAG, dodajmo zajednički ugao GDA. Tada je ceo ugao BDA jednak zbiru uglova GDA i DAG. Ali je zbiru uglova GDA i DAG jednak spoljašnji ugao BGD [I.32]. Prema tome je i ugao BDA jednak uglu BGD. No ugao BDA jednak je uglu GBD, a kako je i strana AD jednaka strani AB [I.5], biće i ugao DBA jednak uglu BGD. Prema tome su tri ugla BDA, DBA, BGD međusobno jednaka. A kako je ugao DBG jednak uglu BGD, biće strana BD jednaka strani DG [I.6]. Ali je BD po pretpostavci jednako GA, pa je, znači, GA jednako GD, dakle i ugao GDA jednak uglu DAG [I.5]. Na taj način je zbir uglova GDA i DAG jednak dvostrukom uglu DAG. A ugao BGD je jednak zbiru uglova GDA i DAG, tj. ugao BGD je dvostruki ugao GAD. Ali je ugao BGD jednak svakom od uglova BDA i DBA, pa je prema tome svaki od uglova BDA i DBA jednak dvostrukom uglu DAB.
Na ovaj način je nacrtan ravnokraki trougao ABD čiji je svaki ugao na osnovici DB dvaput veći od trećeg ugla. A to je trebalo izvesti.