Zbir strane šestougla i desetougla, upisanih u isti krug, podeljen je neprekidno i veći deo je strana šestougla.

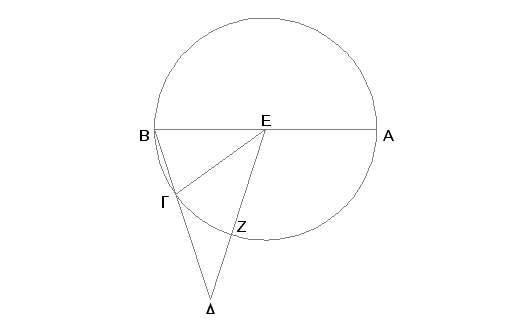
Neka je ABG krug i od slika upisanih u krug ABG neka je BG strana desetougla, a GD - šestougla i neka su nadovezane na istoj pravoj. Tvrdim da se cela BD deli neprekidno i da je veći deo GD.
Zaista, uzmimo za centar tačku E, povucimo EB, EG, ED, i produžimo BE do A. Pošto je BG strana jednakostranog desetougla, luk AGB je pet puta veći od luka BG. Prema tome je luk AG četiri puta veći od luka GB. I luk AG je prema luku GB kao ugao AEG prema uglu GEB [VI.33]. Znači, i ugao AEG je četiri puta veći od ugla GEB. I pošto je ugao EBG jednak uglu EGB [I.5], biće ugao AEG dvaput veći od ugla EGB [I.32]. I pošto je duž EG jednaka duži GD, jer je svaka od njih jednaka strani šestougla upisanog u krug [IV.15, Posledica], biće i ugao GED jednak uglu GDE [I.5], a ugao GEB dvaput veći od ugla EDG [I.32]. A dokazno je da je i ugao AEG dvaput veći od ugla EGB, pa prema tome je ugao AEG četiri puta veći od ugla EDG. Dakle, ugao EDG je jednak uglu BEG. Kod dva trougla BEG i BED ugao EBD je zajednički. I preostali ugao BED jednak je uglu EGB [I.32]. Prema tome trouglovi EBD i EBG imaju jednake uglove. Znači, postoji proporcija: DB je prema BE kao EB pema BG [VI.4]. A EB je jednako GD. Prema tome BD je prema DG kao DG prema GB. I veća je duž BD od DG, pa je i DG veće od GB.
Na taj način duž BD je podeljena (tačkom G) neprekidno i veći njen deo je DG. A to je trebalo dokazati.