12.

Ako je u krug upisan jednakostran trougao, kvadrat na strani tog trougla je triput veći od kvadrata na poluprečniku.

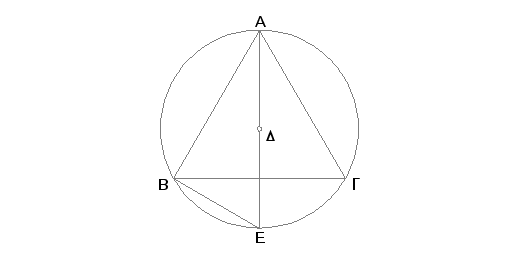
Neka je ABG krug i ABG u nj upisan jednakostran trougao. Tvrdim da je kvadrat na strani trougla ABG jednak trostrukoj vrednosti kvadrata na poluprečniku.
Zaista, uzmimo centar D kruga ABG i pravu što spaja A i D, produžimo do E i nacrtajmo BE. Pošto je trougao ABG jednakostran, biće luk BEG trećina kružnog luka ABG. I pema tome je luk BE šestina kružnog luka ABG. Znači BE je strana šestougla i ona je, na taj način, jednaka poluprečniku [IV.15, Posledica]. A kako je AE dvaput veće od DE, biće kvadrat na AE četiri puta veći od kvadrata na ED, tj. od kvadrata na BE. No kvadrat na AE jednak je zbiru kvadrata na AB i na BE [III.31, I.47]. Znači, zbir kvadrata na AB i na BE jednak je četvorostrukom kvadratu na BE. Stoga, posle oduzimanja, tvrdimo da je kvadrat na AB triput veći od kvadrata na BE. A BE je jednako DE i prema tome kvadrat na AB triput veći od kvadrata na DE.
Na ovaj način je kvadrat na strani trougla triput veći od kvadrata na poluprečniku.