11.

Ako je u krug sa racionalnim prečnikom upisan jednakostran petougao, njegova strana je iracionalna, takozvana ``manja''.

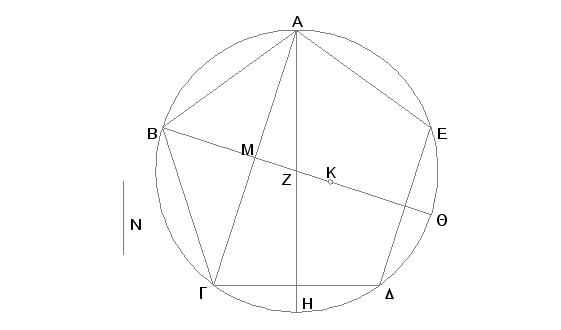
Neka je u krug ABGDE sa racionalnim prečnikom upisan jednakostran petougao ABGDE. Tvrdim da je strana petougla [ABGDE] iracionalna, takozvana ``manja''.
Zaista, uzmimo za centar kruga tačku Z, nacrtajmo AZ i ZB i produžimo ih do tačaka H i Q; nacrtajmo AG i odmerimo ZK, četvrtinu od AZ. AZ je racionalno, pa prema tome je racionalno i ZK. Racionalno je i BZ, a znači racionalno i celo BK. I pošto je luk AGH jednak luku ADH, a jednaki su i njihovi delovi, luk ABG i luk AED, biće i ostatak GH jednak ostatku HD. I ako nacrtamo AD, onda su uglovi kod tačke L pravi i GD je dvaput veće od GL. Iz istih razloga su i kod tačke M uglovi pravi i AG je dvaput veće od GM. Pošto je sad ugao ALG jednak uglu AMZ, ugao LAG zajednički za trouglove AGL i AMZ, biće i preostali ugao AGL jednak preostalom MZA [I.32]. Prema tome trouglovi AGL i AMZ imaju jednake uglove. I na taj način postoji proporcija: LG je prema GA kao MZ prema ZA. I od udvostručenih prethodnih imamo: udvostručeno LG je prema GA kao udvostručeno MZ prema ZA. No udvostručeno MZ je prema ZA kao MZ prema polovini ZA, pa znači udvostručeno LG je prema GA kao MZ prema polovini ZA. I od narednih polovina imamo: udvostručeno LG je prema polovini GA kao MZ prema četvrtini ZA. No udvostručeno LG je DG, a polovina od GA je GM, a četvrtina od ZA je ZK. Prema tome DG je prema GM kao MZ prema ZK. I posle sabiranja: zbir DG i GM je prema GM kao MK prema KZ [V.18]. Dakle, kvadrat na zbiru DG i GM je prema kvadratu na GM kao kvadrat na MK prema kvadratu na KZ. I pošto je kod duži koja spaja dve strane petougla (dijagonale), npr. kod duži AG, podeljene neprekidno, veći deo strana petougla, tj. DG [XIII.8], a kvadrat na zbiru većeg dela i polovine cele duži je pet puta veći od kvadrata na polovini cele duži [XIII.1], i polovina cele AG je GM, biće kvadrat na zbiru DG i GM pet puta veći od kvadrata na GM. Ali, kako je dokazano, kvadrat na zbiru DG i GM se odnosi prema kvadratu na GM kao kvadrat na MK prema kvadratu na KZ. Prema tome je kvadrat na MK pet puta veći od kvadrata na KZ. No KZ je racionalno, jer je racionalan prečnik, pa prema tome je racionalan i kvadrat na MK, dakle, racionalno i MK [ali samo u stepenu]. I pošto je BZ četiri puta veće od ZK, onda je BK pet puta veće od KZ, znači, kvadrat na BK je dvadesetpet puta veći od kvadrata na BZ. No kvadrat na MK je pet puta veći od kvadrata na KZ, dakle, kvadrat na BK je pet puta veći od kvadrata na KM. I prema tome kvadrat na BK prema kvadratu na KM nije u odnosu kvadratnog broja prema kvadratnom broju. Na taj način BK nije samerljivo po dužini sa KM [X.9]. A svako od njih je racionalno. Prema tome su BK i KM racionalne duži, samerljive samo u stepenu. Međutim ako se od racionalne duži oduzme racionalna duž samerljiva sa celom samo u stepenu, biće ostatak iracionalan, apotoma. Znači MB je apotoma, a MK je njena dopuna [X.73]. Tvrdim da je to četvrta apotoma. Neka je ono, za koliko je kvadrat na BK veći od kvadrata na KM, jednako kvadratu na duži N. Znači, kvadrat na BK je veći od kvadrata na KM za kvadrat na N. Pošto je KZ samerljivo sa ZB, biće i sastavljeno KB samerljivo sa ZB [X.15]. Ali BZ je samerljivo sa BQ, pa znači i BK je samerljivo sa BQ [X.12]. I pošto je kvadrat na BK pet puta veći od kvadrata na KM, biće kvadrat na BK prema kvadratu na KM u razmeri 5 prema 1. Prema tome, posle zamene jednog dela drugim, kvadrat na BK prema kvadratu na N je u razmeri 5 prema 4, ne kao kvadratni broj prema kvadratnom broju. Znači, BK nije samerljivo sa N [X.9] i kvadrat na BK je veći od kvadrata na KM za kvadrat na duži koja je nesamerljiva sa BK. Sad, pošto je kvadrat na celoj duži BK veći od kvadrata na njenoj dopuni KM za kvadrat na duži koja je nesamerljiva sa BK, i celo BK je samerljivo sa povučenom racionalnom duži BQ, biće MK četvrta apotoma [X, Def. 14]. I pravougaonik obuhvaćen racionalnom duži i četvrtom apotomom je iracionalan, i strana kvadrata jednakog njegovoj površini je iracionalna, i zove se ``manja'' [X.94]. Duž AB je strana kvadrata jednakog pravougaoniku obuhvaćenom od QB i BM, jer se povlačenjem duži AQ dobija trougao ABQ koji ima sa trouglom ABM jednake uglove, pa će biti QB prema BA kao AB prema BM.
Na ovaj način je AB, strana petougla, iracionalna takozvana ``manja''. A to je trebalo dokazati.