10.

Ako je u krug upisan jednakostran petougao, biće kvadrat strane petougla jednak zbiru kvadrata strane šestougla i strane desetougla upisanih u isti krug.

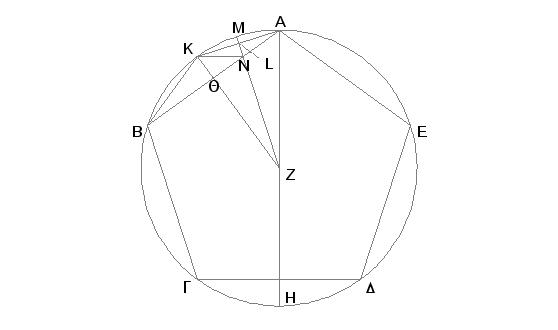
Neka je ABGDE krug i ABGDE jednakostran petougao upisan u krug ABGDE. Tvrdim da je kvadrat strane petougla ABGDE jednak zbiru kvadrata strane šestougla i strane desetougla upisanih u krug ABGDE.
Zaista, uzmimo za centar kruga tačku Z, i produžimo AZ do tačke H, nacrtajmo ZB, i iz tačke Z povucimo normalu ZQ na pravu AB, produžimo je do tačke K, nacrtajmo AK i KB, pa iz tačke Z povucimo ZL, normalu na AK, produžimo je do M i nacrtajmo KN. Pošto je luk ABGH jednak luku AEDH i jednaki su njihovi delovi ABG i AED, biće i ostatak GH jednak ostatku HD. No GD je luk petougla, pa je prema tome GH luk desetougla. I pošto je ZA jednako ZB, a ZQ je normala, biće ugao AZK jednak uglu KZB [I.5, I.26] te prema tome i luk AK jednak luku KB [III.26]. I luk AB je dvaput veći od luka BK, znači, duž AK je strana desetougla. Iz istih razloga i luk AK je dvaput veći od luka KM. I pošto je luk AB dvaput veći od luka BK, a luk GD jednak luku AB, biće i luk GD dvaput veći od luka BK. No luk GD je dvaput veći od luka GH, pa je, znači, i luk GH jednak luku BK. Ali luk BK je dvaput veći od luka KM, kao i luk KA. Pa i luk GH je dvaput veći od KM. No i luk GB je dvaput veći od luka BK, jer je luk GB jednak BA. Znači, ceo luk HB je dvaput veći od BM. Te je prema tome i ugao HZB dvaput veći od ugla ZAB [VI.33]. I na taj način je ugao ZAB jednak uglu ABZ. I ugao BZN jednak je uglu ZAB. Kod dva trougla ABZ i BZN ugao ABZ je zajednički, pa i preostali ugao AZB jednak je preostalom uglu BNZ [I.32]. Dakle trouglovi ABZ i BZN imaju jednake uglove. Znači postoji proporcija: duž AB je prema duži BZ kao duž ZB prema duži BN [VI.4]. I prema tome je pravougaonik obuhvaćen od AB i BN jednak kvadratu na BZ [VI.17]. Zatim, pošto je AL jednako LK, a normala LN je zajednička, biće osnovica KN jednaka osnovici AN [I.4] i ugao LKN jednak uglu LAN. No ugao LAN jednak je uglu KBN, znači i ugao LKN jednak je uglu KBN. I kod dva trougla AKB i AKN ugao kod A je zajednički. Pa i preostali ugao AKB jednak je preostalom uglu KNA [I.32]. Prema tome trouglovi KBA i KNA imaju jednake uglove. Znači, postoji proporcija: duž BA je prema duži AK kao KA prema AN [VI.4]. I pravougaonik obuhvaćen od BA i AN jednak je kvadratu na AK [VI.17]. A dokazano je da je i pravougaonik obuhvaćen od AB i BN jednak kvadratu na BZ. No zbir prvougaonika obuhvaćenog od BA i AN i pravougaonika obuhvaćenog od AB i BN čini kvadrat na BA, koji je prema tome jednak zbiru kvadrata na BZ i na AK. I BA je strana petougla, BZ - šestougla i AK - desetougla.
Na ovaj način, kvadrat strane petougla jednak je zbiru kvadrata strane šestougla i strane desetougla, upisanih u isti krug. A to je trebalo dokazati.