34.
Kod paralelepipeda jednake zapremine osnove su obrnuto proporcionalne visinama. I ako su kod paralelepipeda osnove obrnuto proporcionalne visinama, oni su jednake zapremine.
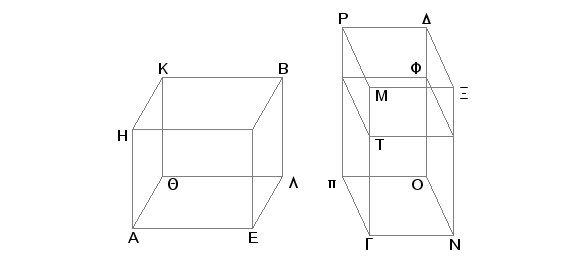
Neka su zapremine paralelepipeda AB i GD jednake. Tvrdim da su osnove paralelepipeda AB i GD obrnuto proporcionalne visinama, i da je osnova EQ prema osnovi NH kao visina tela GD prema visini tala AB.
Zaista, neka su, prvo, bočne ivice AH, EZ, LB, QK, GM, NX, OD, pP normalne na svojim osnovama. Tvrdim, da je osnova EQ prema osnovi Np kao GM prema AH.
Ako je sad osnova EQ jednaka osnovi Np i telo AB jednako telu GD, biće jednaka i duž GM duži AH. Zaista, pralelepipedi iste visine se odnose među sobom kao osnove [XI.32] [jer, ako pri jednakim osnovama EQ i Np visine AH i GM nisu iste, neće biti ni telo AB jednako telu GD. A po pretposravci jednako je. Prema tome visina GM neće biti nejednaka visini AH. Znači jednaka je]. I osnova EQ je prema osnovi Np kao GM prema AH, te je očigledno da su osnove paralelepipeda AB i GD obrnuto proporcionalne visinama.
Neka sad osnova EQ nije jednaka osnovi NH, već je EQ veća. No telo AB je jednako telu GD, pa je stoga, i visina GM veća od visine AH. [jer ako nije, neće tada ni tela AB i GD biti jednaka, a pretpostavljeno je da su jednaka]. Pa odmerimo GT jednako AH i dopunimo na osnovi Np sa visinom GT paralelepiped FG. Pošto je telo AB jednako telu GD, a postoji i telo GF, a jednake (veličine) su u istoj razmeri prema istoj (veličini) [V.7], biće telo AB prema telu GF kao i telo GD prema telu GF. No telo AB je prema telu GF kao osnova EQ prema osnovi Np, jer su tela AB i GF sa istim visinama [XI.32]. Telo GD je prema telu GF kao osnova Mp prema osnovi Tp i visina GM prema visini GT. Prema tome je osnova EQ prema osnovi Np kao visina MG prema visini GT. No GT je jednako AH, i na ovaj način je osnova EQ prema osnovi Np kao MG prema AH. Dakle, osnove paralelepipeda AB i GD obrnuto su proporcionalne visinama.
Dalje, neka osnove paralelepipeda AB i GD budu obrnuto proporcionalne visinama i neka je osnova EQ prema osnovi Np kao visina tela GD prema visini tela AB. Tvrdim da je telo AB jednako telu GD.
[Zaista,] neka su ponovo konstruisane bočne ivice upravne na osnovama. I ako je osnova EQ jednaka osnovi Np, i osnova EQ je prema osnovi Np kao visina tela GD prema visini tela AB, biće visina tela GD jednaka visini tela AB. Pošto su paralelepipedi sa jednakim osnovama i sa istim visinama jednaki među sobom [XI.31], biće telo AB jednako telu GD.
Neka osnova EQ nije jednaka [osnovi] Np, nego je veća EQ. Prema tome je i visina tela GD veća od visine tela AB, tj. GM od AH. Odmerimo ponovo GT jednako AH i na sličan način dopunimo telo GF. Pošto je osnova EQ prema osnovi Mp kao MG prema AH, a AH je jednako GT, biće osnova EQ prema osnovi Mp kao MG prema GT. Ali [osnova] EQ je prema osnovi Np kao telo AB prema telu GF, jer su tela AB i GF sa jednakim visinama [XI.32]. No GM je prema GT kao osnova Mp prema osnovi pT [VI.1] i telo GD prema telu GF [XI.25]. Prema tome je telo AB prema telu GF kao telo GD prema telu GF. Dakle svako od tela AB i GD je u istom odnosu prema GF. Na ovaj način, telo AB je jednako telu GD [V.9]. [A to je trebalo dokazati].
Neka sad konstruisane bočne ivice ZE, BL, HA, QK, XN, DO, MG, Pp nisu upravne na svojim osnovama. Povucimo kroz tačke Z, H, B, K, X, M, D, P normale na ravni EQ i Np i neka njihova podnožja u tim ravnima budu tačke S, T, Y, F, X, Y, W, s pa dopunimo tela ZF i XW. Tvrdim, da su i u tom slučaju, pod uslovima da su tela AB i GD jednaka, osnove obrnuto proporcionalne visinama, naime: osnova EQ je prema osnovi Np kao visina tela GD prema visini tela AB.
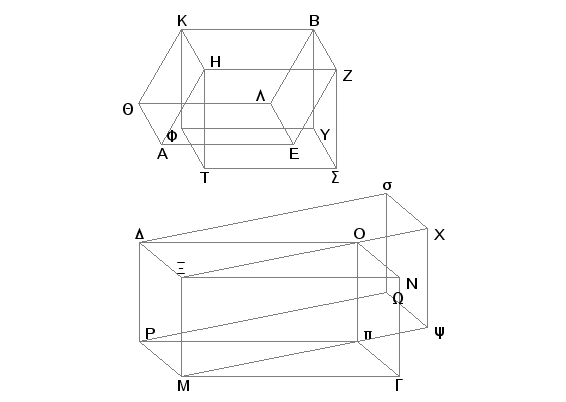
Pošto je telo AB jednako telu GD, a telo AB jednako telu BT, jer su sa istom osnovom ZK i sa istom visinom [XI.29, XI.30] [a krajevi bočnih ivica nisu na istim pravima]. I telo GD jednako je telu DY, jer su opet sa istom osnovom PX i sa istom visinom [XI.29, XI.30] [a krajevi bočnih ivica nisu na istim pravima]. Prema tome i telo BT jednako je telu DY. [Kod jednakih paralelepipeda, pod uslovom da su visine upravne na osnove, osnove su obrnuto proporcionalne visinama]. Prema tome je osnova ZK prema osnovi XP kao visina tela DY prema visini tela BT [na osnovu prvog dela ovog stava]. No osnova ZK je jednaka osnovi EQ, a osnova XP jednaka osnovi Np. Prema tome je osnova EQ prema osnovi Np kao visina tela DY prema visini tela BT. Ali su visine kod tela DY i BT iste kao i kod tela DG i BA. Prema tome je osnova EQ prema osnovi Np kao visina tela DG prema visini tela AB. Na ovaj način, kod paralelepipeda AB i DG osnove su obrnuto proporcionalne visinama.
Neka su sad kod paralelepipeda AB i GD osnove obrnuto proporcionalne visinama, naime: osnova EQ je prema osnovi Np kao visina tela GD prema visini tela AB. Tvrdim da su tela AB i GD jednaka.
Zaista, sa istim konstrukcijama, pošto je osnova EQ prema osnovi Np kao visina tela GD prema visini tela AB, a osnova EQ jednaka je osnovi ZK i osnova Np osnovi XP, biće osnova ZK prema osnovi XP kao visina tela GD prema visini tela AB. Ali su tela AB i GD sa istim visinama kao i tela BT i DY. Prema tome je osnova ZK prema osnovi XP kao visina tela DY prema visini tela BT. Osnove paralelepipeda BT i DY su obrnuto proporcionalne visinama [tela onih paralelepipeda kod kojih su visine upravne na osnovama, a osnove obrnuto proporcionalne visinama, jednaka su]. Prema tome je telo BT jednako telu DY [na osnovu prvog dela ovog stava]. No BT je jednako BA, pošto su sa istom osnovom, ZK, i sa istom visinom [XI.29, XI.30] [a krajevi njihovih bočnih ivica nisu na istim pravim]. I telo DY jednako je telu DG [XI.29, XI.30] [pošto su i ona sa istom osnovom XP i sa istom visinom, a krajevi bočnih ivica nisu na istim pravima].
Na ovaj način, telo AB je jednako telu GD. A to je trebalo dokazati.