33.
Razmera sličnih paralelepipeda je triput viša od razmere homolognih ivica.
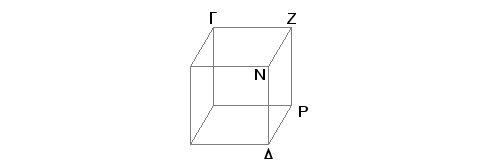
Neka su AB i GD slični paralelepipedi i ivica AE homologna sa ivicom GZ. Tvrdim da je razmera tela AB prema telu GD triput viša od razmere AE prema GZ.
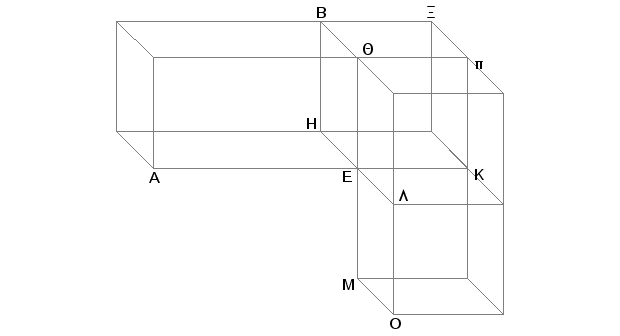
Zaista, produžimo AE, HE i QE za EK, EL i EM i odmerimo EK jednako GZ, EL jednako ZN, EM jednako ZP i dopunimo paralelogram KL i telo KO.
Međutim, kako su dve duži KE i EL jednake dvema dužima GZ i ZN, a i ugao KEL jednak uglu GZN, i ugao AEH jednak uglu GZN zbog sličnosti tela AB i GD, biće jednak [i sličan] paralelogram KL paralelogramu GN. Iz istih razloga je i paralelogram KM jednak i sličan [paralelogramu] GP, i EO - DZ. Prema tome su tri paralelograma tela KO jednaka i slična sa tri paralelograma tela GD. A prva tri su jednaka i slična trima suprotnim, pa i tri druga su jednaka i slična trima suprotnim. Zbog toga je i celo telo KO jednako i slično celom telu GD [XI, Def. 10]. Dopunimo paralelogram HK i na osnovama HK i KL, sa visinom jednakom visini tela AB, dopunimo tela EZ i Lp. Pošto je, zbog sličnosti tela AB i GD, AE prema GZ kao EH prema ZN, i EQ prema ZP i GZ je jednako EK, ZN jednako EL i ZP - EM, biće AE prema EK kao HE prema EL i QE prema EM. No AE je prema EK kao (paralelogram) AH prema paralelogramu HK, HE je prema EL kao HK prema KL, a QE je prema EM kao pE prema KM [VI.1]. Prema tome je paralelogram AH prema HK kao HK prema KL i pE prema KM. No AH je prema HK kao telo AB prema telu EX, a HK je prema KL kao telo XE prema telu pL i pE je prema KM kao telo pL prema telu KO [XI.32]. Prema tome je telo AB prema telu EX kao EX prema pL i pL prema KO. Ali, ako su četiri veličine u neprekidnoj proporciji, biće razmera prve prema četvrtoj triput viša od razmere prve prema drugoj [V, Def. 10]. Prema tome razmera tela AB prema telu KO je triput viša od razmere AB prema EX. No AB je prema EX kao paralelogram AH prema HK i duž AE prema EK [VI.1]. Znači telo AB je prema telu KO u razmeri triput višoj od razmere AE prema EK. No telo KO jednako je telu GD, a duž EK duži GZ i prema tome je razmera tela AB prema telu GD triput viša od razmere ivice AE prema homolognoj ivici GZ.
Na ovaj način, razmera sličnih paralelepipeda je triput viša od razmere homologih ivica. A to je trebalo dokazati.