31.

Paralelepipedi sa jednakim osnovama i istom visinom jednaki su među sobom.

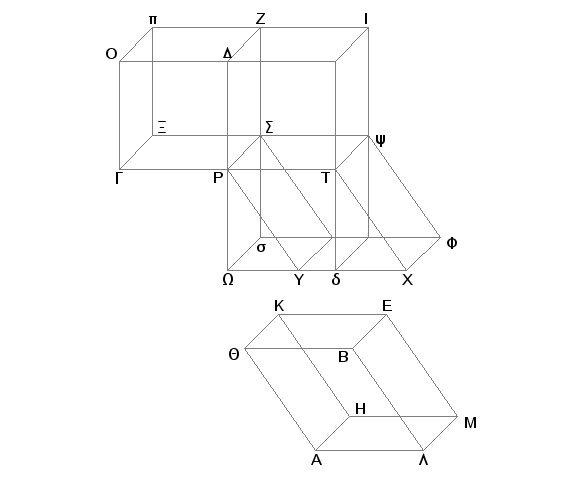
Neka su AE i GZ paralelepipedi sa jednakim osnovama AB i GD i istom visinom. Tvrdim, da je telo AE jednako telu GZ.
Neka su, prvo, bočne ivice QK, BE, AH, LM, Op, DZ, GX, PS upravne na osnovama AB i GD. Odmerimo duž PT u produženju prave GP i konstruišimo na pravoj PT kod tačke P ugao TPY jednak uglu ALB [I.23], odmerimo PT jednako AL i PY jednako LB i dopunimo osnovu PX i telo YY. Pošto su dve strane TP i PY jednake dvema stranama AL i LB, i obuhvaćeni uglovi jednaki, biće jednak i sličan paralelogram PX sa paralelogramom QL. I pošto je, dalje, AL jednako PT, LM jednako PS, a obuhvaćeni uglovi pravi, biće i paralelogram PY jednak i sličan paralelogramu AM. Iz istih razloga je i paralelogram LE jednak i sličan paralelogramu SY. Prema tome su tri paralelograma tela AE jednaka i slična sa tri paralelograma tela YY. A kako su prva tri paralelograma jednaka i slična trima suprotnim, a i druga tri jednaka i slična trima suprotnim [XI.24], biće i ceo paralelepiped AE jednak celom paralelepipedu YY [XI, Def. 10]. Produžimo DP i XY i neka se susreću u tački W. Povucimo kroz T pravu ₁aTd paralelno DW i produžimo OD do ₁a, i dopunimo tela WY i PI. Tada će telo YW kome je osnova paralelogram PY i suprotna strana paralelogram W₁b biti jednako telu YY kome je osnova paralelogram PY i suprotna strana paralelogram YF, jer su ona na istoj osnovi PY, sa istom visinom i bočnim ivicama PW, PY, Td, TX, Ss, Su, Y₁b, YF čiji su krajevi na istim pravama WX i ₁bF [XI.29]. No telo YY jednako je telu AE, pa je prema tome i telo YW jednako telu AE. I pošto je paralelogram PYXT jednak paralelogramu WT, jer su na istoj osnovi i između paralelnih PT i WX [I.35], paralelogram PYXT jednak paralelogramu GD, pošto je jednak i sa AB, biće stoga i paralelogram WT jednak paralelogramu GD. No DT je drugi paralelogram. I prema tome će WT biti prema DT kao osnova GD prema DT [V.7]. A pošto je paralelepiped GI presečen sa ravni PZ paralelno sa suprotnim stranama, biće osnova GD prema osnovi DT kao telo GZ prema telu PI [XI.25]. Iz istih razloga će, pošto je WI presečen sa ravni PY paralelno sa suprotnim stranama, biti osnova WT prema osnovi TD kao telo WY prema telu PI [XI.25]. No osnova GD je prema DT kao WT prema DT. Dakle, i telo GZ je prema telu PI kao telo WY prema telu PI [V.11]. Prema tome je svako od tela GZ i WY u istom odnosu prema telu PI. Stoga je telo GZ jednako telu WY. No telo WY je, kako je dokazano, jednako telu AE. Na ovaj način telo AE jednako je telu GZ.

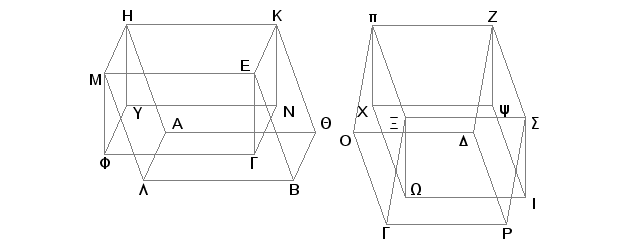
Neka sad bočne ivice AH, QK, BE, LM, GX, Op, DZ, PS nisu upravne na osnovama AB i GD. Opet tvrdim da je telo AE jednako telu GZ. Zaista, spustimo iz tačaka K, E, H, M, p, Z, X, S normale KN, EG, HY, MF, pX, ZY, XW, SI na osnovnu ravan i neka su podnožja tih normala tačke N, G, Y, F, X, Y, W, I i spojimo NG, NY, YF, GF, XY, XW, WI, IY. Telo KF je tada jednako telu pI, jer su ona sa jednakim osnovama KM i pS, istom visinom i bočnim ivicama upravnim na osnovama [na osnovu prvog dela ovog stava]. Ali i telo KF jednako je telu AE, a telo pI telu GZ, pošto su ona sa istom osnovom, istom visinom i bočnim ivicama čiji se krajevi ne nalaze na istim pravima [XI.30]. Prema tome i telo AE jednako je telu GZ.
Na ovaj način, paralelepipedi sa jednakim osnovama i istim visinama jednaki su među sobom. A to je trebalo dokazati.