4.
U dati trougao upisati krug.
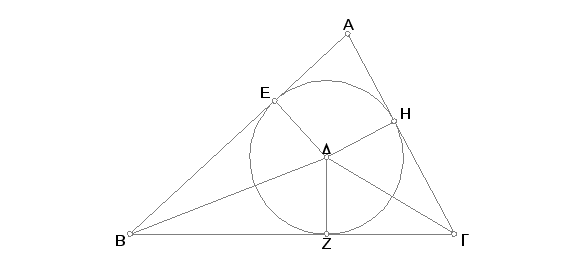
Prepolovimo uglove ABG i AGB pravama BD i GD i neka se te prave seku u tački D, pa povucimo iz tačke D na prave AB, BG, GA normale DE, DZ, DH.
Kako je ugao ABD jednak uglu GBD, a pravi ugao BED jednak pravom uglu BZD, dva trougla EBD i ZBD imaće po dva ugla jednaka i po jednu stranu jednaku, i to spram jednakih uglova, naime zajedničku stranu BD; prema tome će i ostale strane jednog biti jednake ostalim stranama drugog [I.26]; biće dakle DE jednako DZ. Na osnovu istih razloga je i DH jednako DZ. Znači da su tri prave DE, DZ, DH međusobno jednake. Prema tome će krug sa centrom u D opisan sa rastojanjem do jedne od tačaka E, Z, H kao poluprečnikom proći i kroz ostale tačke i u tačkama E, Z, H dodirivati prave AB, BG, GA, jer su uglovi u tim tačkama pravi. Zaista, kad bi on sekao te prave, onda bi normala na prečnik, što prolazi kroz njegov kraj, bila u krugu, a to je, kao što je dokazano, nemoguće [III.16]. Prema tome krug sa centrom u D opisan sa rastojanjem do koje bilo od tačaka E, Z, H ne seče prave AB, BG, GA. Dakle on ih dodiruje i biće krug upisan u trougao ABG [IV, Def. 5]. Neka je on upisan kao ZHE.
Na ovaj način je u dati trougao ABG upisan krug EZH. A to je trebalo izvesti.