12.

Oko datog kruga opisati petougao sa jednakim stranama i jednakim uglovima.

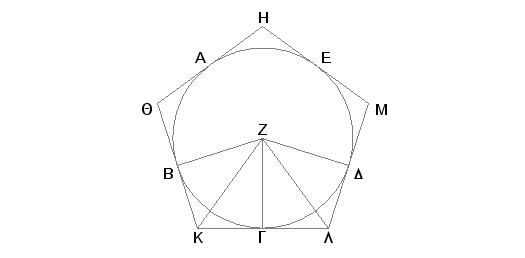
Neka je dat krug ABGDE. Treba oko kruga ABGDE opisati petougao sa jednakim stranama i jednakim uglovima.
Zamislimo da se u tačkama A, B, G, D, E nalaze temena upisanog petougla, tada su luci AB, BG, GD, DE, EA jednaki [IV.11]. Kroz tačke A, B, G, D, E povucimo tangente HQ, QK, KL, LM, MH na krug [III.16, Posledica], i uzmimo krug ABGDE sa centrom u Z [III.1] i povucimo ZB, ZK, ZG, ZL, ZD.
Kako prava KL dodiruje krug ABGDE u tački G, a ZG je prava povučena iz centra Z kroz tačku dodira G, biće ZG normalno na KL [III.18]. Prema tome je svaki od uglova kod tačke G prav. Iz istih razloga su uglovi i kod tačaka B i D pravi. A kako je ugao ZGK prav, biće kvadrat na ZK jednak zbiru kvadrata na ZG i na GK [I.47]. Iz istih razloga je zbir kvadrata na ZB i na BK jednak kvadratu na ZK. Prema tome je zbir kvadrata na ZG i na GK jednak zbiru kvadrata na ZB i BK, a kako je kvadrat na ZG jednak kvadratu na ZB, biće i preostali kvadrat na GK jednak preostalom kvadratu na BK. Odavde je i BK jednako GK. A kako je ZB jednako ZG, a ZK je zajedničko, dve strane BZ i ZK jednake su dvema stranama GZ i ZK, a i osnovica BK je jednaka osnovici GK, stoga je i ugao BZK jednak uglu KZG [I.8] i ugao BKZ jednak uglu ZKG. Znači ugao BZG je dvaput veći od ugla KZG, a ugao BKG je dvaput veći od ugla ZKG. Iz istih razloga je ugao GZD dvaput veći od ugla GZL, a i ugao DLG od ugla ZLG. A kako je luk BG jednak luku GD, biće i ugao BZG jednak uglu GZD [III.27]. No kako je i ugao BZG dvaput veći od ugla KZG, a DZG od ugla LZG, biće ugao KZG jednak uglu LZG, a jednak je i ugao ZGK uglu ZGL. Dva trougla ZKG i ZLG imaju dakle po dva ugla jednaka i po jednu stranu jednaku, naime zajedničku stranu ZG. Znači i ostale strane jednog trougla jednake su ostalim stranama drugog, i preostali ugao jednog jednak preostalom uglu drugog [I.26]. Prema tome je prava KG jednaka pravoj GL i ugao ZKG jednak uglu ZLG. Kako je KG jednako GL, KL će biti jednako dvaput KG. Na isti način se dokazuje da je i QK dvaput BK. A kako je BK jednako KG, biće i QK jednako KL. Na sličan način se dokazuje da je svaka od pravih QH, HM, ML jednaka svakoj od QK i KL. Petougao HQKLM je prema tome sa jednakim stranama. Tvrdim da je on i sa jednakim uglovima. Zaista, kako je ugao ZKG jednak uglu ZLG, a dokazano je da ugao je QKL dvaput veći od ugla ZKG, i ugao KLM dvaput veći od ugla ZLG, biće i ugao QKL jednak uglu KLM. Na sličan način se dokazuje da je i svaki od uglova KQH, QHM, HML jednak svakom od QKL i KLM. Prema tome su pet uglova HQK, QKL, KLM, LMH, MHQ međusobno jednaki. Petougao HQKLM je prema tome sa jednakim uglovima. A dokazano je da i sa jednakim stranama, i da je opisan oko kruga ABGDE.
Na ovaj način je oko datog kruga opisan petougao sa jednakim stranama i jednakim uglovima. A to je trebalo izvesti.