36.
Ako je van kruga uzeta neka tačka i iz te tačke su povučene ka krugu dve prave, od kojih jedna seče krug, a druga ga dodiruje, onda je pravougaonik od cele sečice i njenog otsečka između uzete tačke i ispupčenog luka jednak kvadratu na tangenti.
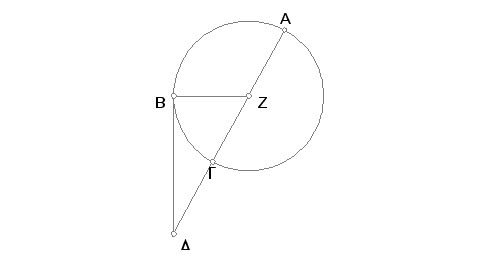
Uzmimo tačku D van kruga ABG i iz tačke D povucimo na krugu ABG dve prave DG(A) i DB, pri čemu prava DGA seče krug, a BD ga dodiruje. Tvrdim, da je pravougaonik obuhvaćen od AD i DG jednak kvadratu na DB.
Prava (D)GA ili prolazi kroz ili ne prolazi. Neka, prvo, prolazi kroz centar i neka Z bude centar kruga ABG, pa povucimo ZB. Tada je ugao ZBD prav [III.18]. Pošto tačka Z polovi duž AG, a GD je njeno produženje, biće pravougaonik od AD i DG sa kvadratom na ZG jednak kvadratu na ZD [II.6]. Ali ZG je jednako ZB. Prema tome, pravougaonik od AD i DG sa kvadratom na ZB jednak je kvadratu na ZD. Međutim, kvadrat na ZD jednak je zbiru kvadrata na ZB i na BD [I.47]. To znači da je pravougaonik od AD i DG sa kvadratom na ZB jednak zbiru kvadrata na ZB i na BD. Oduzmimo zajednički kvadrat na ZB. Tada je ostatak, pravougaonik na AD i DG, jednak kvadratu na tangenti DB.
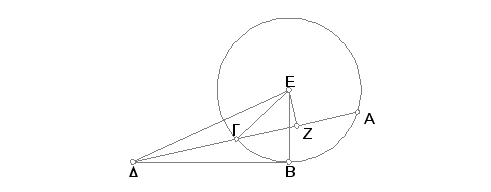
Neka sad DGA ne prolazi kroz centar kruga ABG; uzmimo centar E i iz tačke E spustimo normalu EZ na pravu AG, i povucimo EB, EG, ED. Tada je ugao EBD prav [III.18]. Kako prava EZ, koja prolazi kroz centar, seče pravu AG, koja ne prolazi kroz centar, i polovi je [III.3], biće AZ jednako ZG. I pošto je prava AG prepolovljena tačkom Z, a GD je njeno produženje, biće pravougaonik od AD i DG sa kvadratom na ZG jednak kvadratu na ZD [II.6]. Dodajmo im kvadrat na ZE. Tada je pravougaonik od AD i DG sa kvadratima na GZ i na ZE jednak zbiru kvadrata na ZD i na ZE. Ali zbir kvadrata na GZ i na ZE jednak je kvadratu na EG, jer je ugao EZG prav [I.47]. I zbir kvadrata na DZ i na ZA je jednak kvadratu na ED. Stoga je pravougaonik od AD i DG sa kvadratom na EG jednak kvadratu na ED. Ali EG je jednako EB. Prema tome je pravougaonik od AD i DG sa kvadratom na EB jednak kvadratu na ED. Ali kvadrat na ED je jednak zbiru kvadrata na EB i na BD, jer je ugao EBD prav [I.47]. Stoga je pravougaonik od AD i DG sa kvadratom na EB jednak zbiru kvadrata na EB i na BD. Oduzmimo sad zajednički kvadrat na EB. Tada je ostatak, pravougaonik na AD i DG jednak kvadratu na DB.
Na ovaj način, ako je van kruga uzeta neka tačka i iz te tačke su povučene ka krugu dve prave, od kojih jedna seče krug, a druga ga dodiruje, ondaje pravougaonik od cele sečice i njenog otsečka između uzete tačke i ispupčenog luka jednak kvadratu na tangenti. A to je trebalo dokazati.