35.
Ako se u krugu dve tetive međusobno seku, biće pravougaonik obuhvaćen otsečcima jedne tetive jednak pravougaoniku obuhvaćenom otsečcima druge.
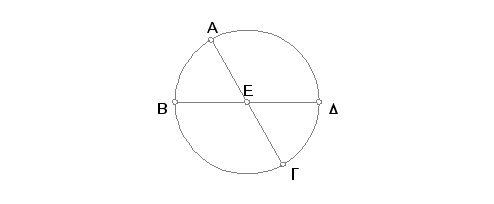
Neka se u krugu ABGD dve tetive AG i BD međusobno seku u tački E. Tvrdim da je pravougaonik obuhvaćen od AE i EG jednak pravougaoniku obuhvaćenom od DE i EB.
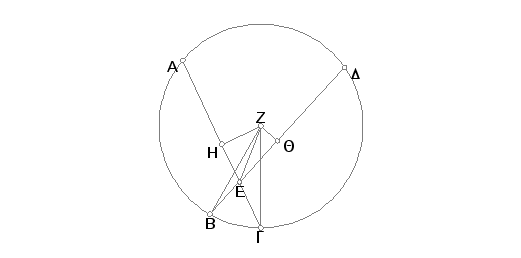
Ako tetive AG, BD prolaze kroz centar kruga, onda je jasno da su duži AE, EG, DE, EB jednake i da je pravougaonik obuhvaćen od AE i EG jednak pravougaoniku obuhvaćenom DE i EB.
Neka sad AG i DB ne prolaze kroz centar; uzmimo centar kruga ABGD, neka to bude tačka Z; spustimo iz tačke Z normale ZH i ZQ na prave AG i DB i povucimo ZB, ZG, ZE.
Kako prava HZ koja prolazi kroz centar, seče pravu AG, koja ne prolazi kroz centar, pod pravim uglovima, onda ona polovi tu pravu [III.3], pa će AH biti jednako HG. Pošto tačka H polovi duž AG, a tačka E je ne deli na nejednake delove, biće pravougaonik obuhvaćen od AE i EG sa kvadratom na EH jednak kvadratu HG [II.5]. Dodajmo im kvadrat na HZ. Tada je pravougaonik od AE i EG zajedno sa kvadratima na HE i na HZ jednak zbiru kvadrata na GH i na HZ. Ali zbir kvadrata na EH i na HZ jednak je kvadratu na ZE i zbir kvadrata na GH i na HZ jednak je kvadratu na ZG [I.47]. Prema tome pravougaonik od AE i EG sa kvadratom na ZE jednak je kvadratu na ZG. Ali ZG je jednako ZB. Stoga je pravougaonik od AE i EG sa kvadratom na ZE jednak kvadratu na ZB. Iz istih razloga je pravougaonik od DE i EB zajedno sa kvadratom na ZE jednak kvadratu na ZB. A dokazali smo da je pravougaonik od AE i EG sa kvadratom na ZE jednak kvadratu na ZB. Odavde sleduje da je pravougaonik od AE i EG sa kvadratom na ZE jednak pravougaoniku od DE i EB sa kvadratom na ZE. Oduzmimo zajednički kvadrat na ZE. Tada je ostatak, pravougaonik od AE i EG, jednak pravougaoniku od AE i EB.
Na ovaj način, ako se u krugu dve tetive međusobno seku, biće pravougaonik obuhvaćen otsečima jedne tetive jednak pravougaoniku obuhvaćenom otsečima druge. A to je trebalo dokazati.