Povećavanje stepena Bézier-ove krive

Mnoge aplikacije koje koriste dve i više Bézier-ovih krivih zahtevaju da sve krive budu istog stepena. Štaviše, iako Bézier-ove krive višeg stepena zahtevaju više vremena za obradu, one su pogodnije za dizajniranje različitih oblika. Stoga bi bilo od velike pomoći da se povisi stepen Bézier-ovih krivih bez promene njihovog oblika. Primetimo da je "ne menjanje oblika krive" ključni zahtev; u suprotnom, povećavanje stepena Bézier-ove krive ne bi imalo praktičnog smisla.

Pretpostavimo da imamo Bézier-ovu krivu stepena n određenu sa n + 1 kontrolnih tačaka P₀, P₁, P₂,..., P_n i da želimo da povisimo njen stepen za 1 bez promene njenog oblika. Kako je Bézier-ova kriva (n + 1). stepena definisana sa n + 2 kontrolne tačke, potrebno je da nađemo takav novi skup kontrolnih tačaka. Očigledno, tačke P₀ i P_n moraju pripadati novom skupu jer kriva prolazi kroz njih. Stoga, potrebno je izračunati samo n novih tačaka. Neka je Q₀, Q₁, Q₂,..., Q_n+1 novi skup kontrolnih tačaka. Tada je Q₀ = P₀ i Q_n+1 = P_n, a ostale tačke se određuju po sledećoj formuli:

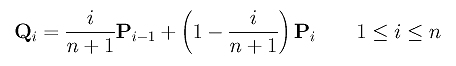
Svaka duž početne poligonalne linije sadrži tačno jednu novu kontrolnu tačku. Preciznije, duž P_i-1P_i sadrži novu kontrolnu tačku Q_i. Iz formule za računanje novih kontrolnih tačaka, vidimo da Q_i deli duž P_i-1P_i u odnosu 1 - i/(n+1):i/(n+1). Za razliku od de Casteljau-ovog algoritma, ovaj odnos nije konstantan, već zavisi od vrednosti i. Ipak, račun je veoma sličan onom iz de Casteljau-ovog algoritma.

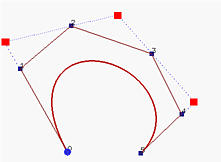
Kada dobijemo skup kontrolnih tačaka, početni skup može biti odbačen. Kako svaka duž početne poligonalne linije sadrži novu kontrolnu tačku, proces zamene starog skupa novim može se posmatrati kao odsecanje uglova u početnim kontrolnim tačkama. Sledeća slika ilustruje ovaj efekat odsecanja uglova. Na njoj je prikazana Bézier-ova kriva 4. stepena, čije su kontrolne tačke označene crvenim kvadratima, a kontrolna poligonalna linija plavom isprekidanom linijom. U levoj tabeli prikazan je odnos na svakoj duži početne poligonalne linije.

i 1 - i/(n+1) 1 0.8 2 0.6 3 0.4 4 0.2

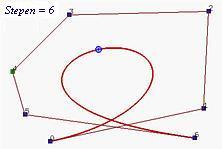
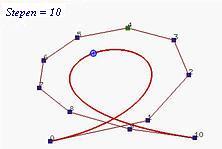
Primetimo da se stepen krive može povećavati dok god to sistem dozvoljava, pri čemu se sa povećanjem broja kontrolnih tačaka poligonalna linija približava krivoj. Na sledećim slikama predstavljeno je povećanje stepena početne krive 6. stepena sa 7 kontrolnih tačaka na 7, 8, 10, 15 i 29. Kao što se može primetiti sa slika, oblik krive ostaje nepromenjen sa povećanjem stepena, ali se poligonalna linija sve više probližava krivoj.