Određivanje tačke na Bézier-ovoj krivoj: De Casteljau-ov algoritam

Jednostavan način rešavanja problema određivanja tačke C(u) na Bézier-ovoj krivoj za neko u je zamena u u jednačini krive, ali ovaj način je numerički nestabilan - dolazi do greške pri računanju Bernstein-ovih polinoma.

Označimo kontrolne tačke na sledeći način: P₀ sa 00, P₁ sa 01, ... , P_i sa 0i, ... , P_n sa 0n, gde prva cifra označava broj iteracije (ovde je 0, a kasnije će biti 1,2,3 itd.).

Osnovna ideja de Casteljau-ovog algoritma je izbor tačke C na duži AB takve da C deli duž AB u odnosu u:1-u. Kako se u kreće od 0 do 1, tačka C data sa A + u(B - A) = (1 - u)A + uB jeste tačka duži AB koja je deli u traženom odnosu.

De Casteljau-ov algoritam:

Pretpostavimo da želimo da odredimo tačku C(u), gde je u u intervalu [0,1]. Počinjemo od poligonalne linije 00-01-02-03-...-0n i koristeći prethodnu formulu nalazimo tačku 1i koja deli duž određenu tačkama 0i i 0(i+1) u odnosu u:1-u. Na ovaj način dobijamo n tačaka 10, 11, 12, ...., 1(n-1) koje definišu novu poligonalnu liniju sastavljenu od n - 1 duži. Primenjujući prethodni postupak na novu poligonalnu liniju dobijamo i drugu liniju od n - 1 tačaka 20, 21, ... , 2(n-2) i n - 2 duži. Ponavljajući ovaj proces n puta, dobijamo jednu tačku n0. De Casteljau je dokazao da je upravo to tačka C(u) na krivoj koja odgovara u.

Primer:
Na slici je predstavljena kriva 5. stepena.
Odredimo za u=0.4 tačke 10 na duži 00-01, 11 na duži 01-02, ... , i 14 na 04-05, takve da dele odgovarajuće duži u odnosu 0.4 : 0.6, tj. 2:3.
Neka je 20 tačka koja u zadatom odnosu deli duž 10-11. Slično, izaberimo tačku 21 na duži 11-12, 22 na duži 12-13 i 23 na 13-14. Tako smo dobili i treću poligonalnu liniju određenu tačkama 20, 21, 22 i 23. Ova linija ima 4 temena i 3 duži.
Nastavljajući ovaj postupak dobićemo poligonalnu liniju sa tri temena 30, 31 i 32.
Iz četvrte poligonalne linije dobijamo petu sa dve tačke 40 i 41.
Poslednja iteracija daje teme 50 koje odgovara tački C(0.4) na krivoj.

Implementacija

Uzimajući u obzir prethodno izloženu interpretaciju de Casteljau-ovog algoritma, izračunavanje se vrši po principu prikazanom na slici:

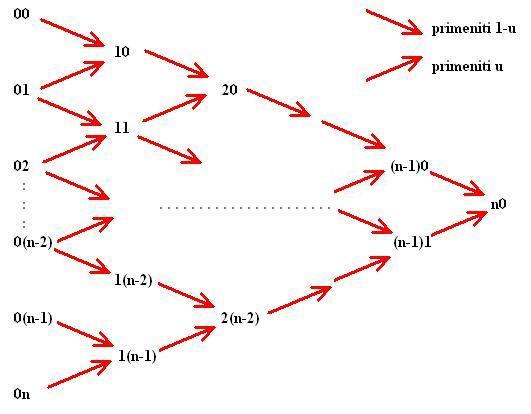
Prvo, sve kontrolne tačke rasporedimo u kolonu. Iz početne kolone 0 izračunavamo kolonu 1; iz kolone 1 dobijamo kolonu 2 i tako dalje. Konačno, nakon n iteracija dobijamo jednu tačku n0 i to je tražena tačka krive. Naredni algoritam sumira prethodnu diskusiju. Kao ulazne podatke uzima niz P od n+1 kontrolne tačke i u između 0 i 1, a vraća tačku na Bézier-ovoj krivoj C(u).

Ulaz: niz P[0:n] od n+1 tačaka i realni broj u iz [0,1]
Izlaz: tačka na krivoj, C(u)
Pomoćne promenljive: niz tačaka Q[0:n]

for i := 0 to n do
Q[i] := P[i]; // save input
for k := 1 to n do
for i := 0 to n - k do
Q[i] := (1 - u)Q[i] + u Q[i + 1];
return Q[0];

Rekurzija

Prethodno izračunavanje može se izvršiti rekurzivno. Stavimo da P_0,j budu kontrolne tačke P_j, za j = 0, 1, ..., n, tj. P_0,j je j-ti član u koloni 0. Na sledeći način računamo j u koloni i:

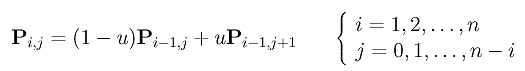
Preciznije, vrednost P_i,j je zbir (1-u)P_i-1,j (gore levo) i uP_i-1,j+1 (dole levo). Krajnji rezultat (i.e., tačka na krivoj) je P_n,0. Koristeći ovu ideju, formiramo rekurzivnu proceduru:

function deCasteljau(i,j)
begin

if i = 0 then

return P_0,j

else

return (1-u)*deCasteljau(i-1,j) + u*deCasteljau(i-1,j+1)
end

Iako procedura deluje jednostavno i kratko, veoma je neefikasna. Da bi izračunali P_n,0, pozivamo funkciju deCasteljau(n,0), a ona se u else delu poziva još dva puta. Problem je u tome što se skoro sve funkcije za računanje P_i,j pozivaju više od jednom.

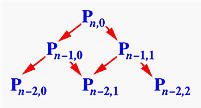
Koliko je to loše? Složenost ovog izračunavanja istovetna je složenosti izračunavanja n-tog člana Fibonacci-jevog niza.

function Fibonacci(n)
begin
if n = 0 or n = 1 then

return 1

else
return Fibonacci(n-1) + Fibonacci(n-2)
end

Broj poziva funkcije Fibonacci(n) eksponencijalno raste! Zbog toga, rekurzivna verzija Casteljau-ovog algoritma nije pogodna za direktnu implementaciju!