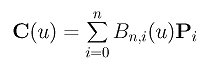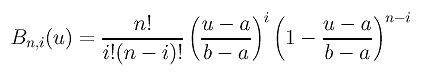Konstrukcija Bézier-ovih krivih

Neka su P0,P1,P2,
...,Pn tačke u ravni.
Bézier-ova krive stepena n definisana ovim
kontrolnim tačkama Pi je
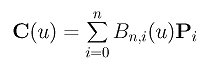
gde su koeficijenti Bn,i(u) Bernstein-ovi polinomi definisani sa:

Osnovna svojstva Bézier-ovih krivih:
- Stepen Bézier-ove krive definisane sa n+1
kontrolnih tačaka je n:
U svakoj baznoj funkciji stepen od u je i +
(n - i) = n. Stoga, stepen
krive je n.
- C(u) prolazi kroz tačke P0 i
Pn:
Jednostavnim računom može sa proveriti da kriva prolazi kroz prvu i poslednju kontrolnu tačku.
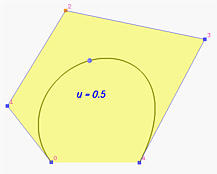
- Nenegativnost:
Primetimo da se u nalazi u intervalu [0,1], pa su sve bazne funkcije
nenegativne.
- Svojstvo konveksnog omotača:
Bézier-ova kriva određena sa datih
n + 1 kontrolnih tačaka leži unutar konveksnog omotača tih tačaka.
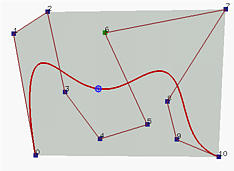
Na slici je prikazana Bézier-ova kriva 10. stepena, a konveksni omotač njenih 11
kontrolnih tačaka označen je sivom bojom. Čitava kriva leži unutar konveksnog omotača,
osim dve krajnje tačke koje su na rubu.
- Svojstvo manje varijacije:
Za krivu u ravni, ovo svojstvo znači da
ni jedna prava ne preseca Bézier-ovu krivu više puta nego što seče kontrolnu poligonalnu liniju.

Na slici, žuta linija preseca krivu 3 puta i poligonalnu liniju 7 puta;
zelena linija seče kkrivu 5, a poligonalnu liniju 7 puta; a
plava linija ima po dve presečne tačke i sa krivom i sa poligonalnom linijom.
Ovo svojstvo nam govori da je kontrolna poligonalna linija kompleksnija od krive koju određuje.
Naime, poligonalna linija se češće uvrće i skreće, nego što je to slučaj sa Bézier-ovom krivom.
- Afina invarijantnost:
Rezultat primene afinih transformacija na Bézier-ovu krivu je kriva koja može biti konstruisana
na osnovu slika kontrolnih tačaka pri zadatim transformacijama.
Dakle, kada želimo da primenimo afine transformacije na Bézier-ovu krivu, jednostavno ih primenimo
na kontrolne tačke (što je znatno lakše), a traženu krivu formiramo na osnovu novih, izmenjenih
kontrolnih tačaka.

Šta ako u nije definisano na [0,1]?
U slučaju da je domen Bézier-ove krive [a,b], potrebno je izvršiti smenu promenljive
u na sledeći način:

Nova promenljiva u definisana je na intervalu [0,1] i njenom zamenom
u baznim funkcijama Bn,i(u) dobijamo:
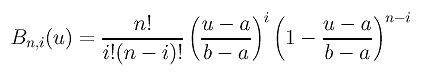
Nove bazne funkcije definišu Bézier-ovu krivu na intervalu [a,b].
 konstrukcija krivih
... pomeranje kontrolnih tačaka
... određivanje tačke na krivoj
... podela krive na dva dela
... povećavanje stepena krive
... Bézier-ove krive i površi
konstrukcija krivih
... pomeranje kontrolnih tačaka
... određivanje tačke na krivoj
... podela krive na dva dela
... povećavanje stepena krive
... Bézier-ove krive i površi