Neka su dati: krug  , prava
, prava  i tačka A. Traženi krug O treba da dodiruje dati krug
i tačka A. Traženi krug O treba da dodiruje dati krug  , datu pravu
, datu pravu  i prolazi kroz datu tačku A (sl. 21).
i prolazi kroz datu tačku A (sl. 21).
- Analiza: Ako iz centra
 datog kruga spustimo normalu
datog kruga spustimo normalu 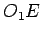 na datu pravu
na datu pravu  i krajeve odgovarajućeg prečnika označimo sa C i D, pojedine operacije možemo tumačiti na sledeći i način:
i krajeve odgovarajućeg prečnika označimo sa C i D, pojedine operacije možemo tumačiti na sledeći i način:
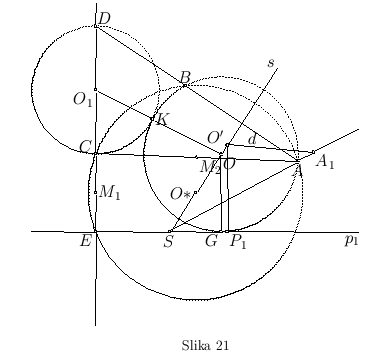
1. Dat je krug  sa tačkom E, koja je projekcija tačaka C,
sa tačkom E, koja je projekcija tačaka C,  i D na pravoj
i D na pravoj  . Tačka
. Tačka 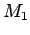 je središte duži CE, a tačka
je središte duži CE, a tačka 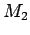 središte duži CA.
središte duži CA.
2. Krug ACE sa centrom 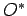 određuje se kao u zadatku 16.
određuje se kao u zadatku 16.
3. Presečna tačka prave DA i kruga ACE određuje tačku B na tom krugu.
4. Dve tačke A i B određuju simetralu s tetive AB, a presečna tačka ove simetrale sa pravom  je tačka S.
je tačka S.
5. Na simetrali s uzmimo proizvoljnu tačku 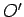 .
.
6. Odmeravamo rastojanje tačke O' od prave  . Označimo to rastojanje sa
. Označimo to rastojanje sa 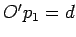 .
.
7. Na produženju SA određujemo tačku 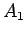 sa rastojanjem d od tačke
sa rastojanjem d od tačke 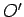 .
.
8. Iz tačke A konstruišemo pravu paralelnu sa 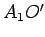 . Ova prava se seče sa simetralom s u tački O, a to je centar traženog kruga, koji prolazi kroz A, B, K, G, gde su K i G dodirne tačke sa datim krugom i datom pravom.
. Ova prava se seče sa simetralom s u tački O, a to je centar traženog kruga, koji prolazi kroz A, B, K, G, gde su K i G dodirne tačke sa datim krugom i datom pravom.
- Konstrukcija: Konsrukcija neposredno sledi iz analize i u slučaju kada traženi krug sa unutrašnje strane dodiruje dati krug.
- Dokaz: Elementi dokaza nalaze se u analizi.
- Diskusija: U ovom zadatku, zbog raznolikosti datih elemenata - kruga, prave i tačke, u proizvoljnim položajima, specijalni slučajevi su mnogobrojni, pa nećemo ulaziti detaljno u sve mogućnosti. Međutim, obratićemo pažnju na metodu koja je bila primenjena pri rešavanju ovog zadatka. Ona se sastoji u uvođenju nekog novog geometrijskog objekta koji spaja raznovrsne date elemente. Pri rešavanju ovog zadatka bio je uveden krug ACE, pomoćne uloge, koji spaja datu tačku A, datu pravu
 i dati krug
i dati krug  . Spajanje tačke A sa D određuje tačku B, koja rešava problem.
. Spajanje tačke A sa D određuje tačku B, koja rešava problem.
2005-04-12
![]() , prava
, prava ![]() i tačka A. Traženi krug O treba da dodiruje dati krug
i tačka A. Traženi krug O treba da dodiruje dati krug ![]() , datu pravu
, datu pravu ![]() i prolazi kroz datu tačku A (sl. 21).
i prolazi kroz datu tačku A (sl. 21).
