Neka su  i
i  dve date prave i
dve date prave i  dati krug (sl. 12).
dati krug (sl. 12).
- Analiza: Treba konstruisati krug koji dodiruje date prave
 i
i  i krug
i krug  poluprečnika R. Njemu koncentričnan krug, poluprečnika r+R prolazi kroz centar
poluprečnika R. Njemu koncentričnan krug, poluprečnika r+R prolazi kroz centar  datog kruga i dodiruje prave
datog kruga i dodiruje prave 
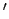 i
i 
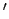 , paralelne pravama
, paralelne pravama  i
i  , na odstojanju R od njih. Prema tome, zadatak se svodi na konstukciju kruga koji dodiruje dve date prave
, na odstojanju R od njih. Prema tome, zadatak se svodi na konstukciju kruga koji dodiruje dve date prave 
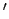 i
i 
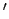 i prolazi kroz datu tačku
i prolazi kroz datu tačku  , odnosno tačku A, a to je zadatak 4. Kako smo videli u zadatku 4, kroz tačku A možemo povući dva kruga koji dodiruju prave
, odnosno tačku A, a to je zadatak 4. Kako smo videli u zadatku 4, kroz tačku A možemo povući dva kruga koji dodiruju prave 
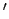 i
i 
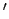 , pa prema tome, imamo i dva kruga koji dodiruju prave
, pa prema tome, imamo i dva kruga koji dodiruju prave  i
i  i spolja krug
i spolja krug  . Sem toga, povukli smo i dve prave
. Sem toga, povukli smo i dve prave 
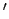 i
i 
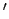 izvan ugla datih pravih
izvan ugla datih pravih  i
i  , ali možemo uzeti u obzir krugove koji isto tako dodiruju prave
, ali možemo uzeti u obzir krugove koji isto tako dodiruju prave  i
i  , ali krug
, ali krug  dodiruju iznutra. U tom slučaju, koncentrične krugove k(O, r) i k(O, r+R) dodiruju prave paralelne pravama
dodiruju iznutra. U tom slučaju, koncentrične krugove k(O, r) i k(O, r+R) dodiruju prave paralelne pravama  i
i  , ali ne one koje se nalaze spolja, već u uglu. Označimo ih sa
, ali ne one koje se nalaze spolja, već u uglu. Označimo ih sa 
 i
i 
 (ove dve prave nisu predstavljene na slici).
(ove dve prave nisu predstavljene na slici).
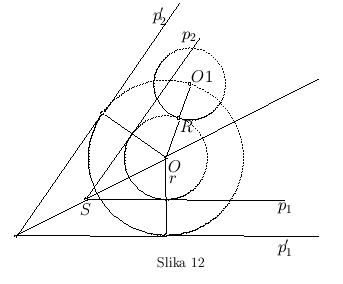
- Konstrukcija: Konstruišimo najpre van datog ugla dve prave

 i
i 
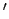 paralelne pravama
paralelne pravama  i
i  , na rastojanju R od njih. Kroz centar datog kruga povucimo dva kruga koji dodiruju prave
, na rastojanju R od njih. Kroz centar datog kruga povucimo dva kruga koji dodiruju prave 
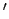 i
i 
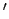 (na slici je prikazan samo jedan od njih) 5. Neka centri tih krugova budu u tačkama
(na slici je prikazan samo jedan od njih) 5. Neka centri tih krugova budu u tačkama  i
i 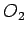 . Sa tim centrima konstruišimo koncentrične krugove poluprečnika smanjenih za poluprečnik datog kruga. Dobijena dva koncentrična kruga odgovaraju uslovima zadatka.
. Sa tim centrima konstruišimo koncentrične krugove poluprečnika smanjenih za poluprečnik datog kruga. Dobijena dva koncentrična kruga odgovaraju uslovima zadatka.
Na sličan način, ako povučemo paralelne prave 
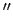 i
i 
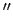 , u datom uglu i ponovo prema zadatku 4. konstruišemo dva kruga koji dodiruju te prave i prolaze kroz centar datog kruga, onda ćemo dobiti dva centra
, u datom uglu i ponovo prema zadatku 4. konstruišemo dva kruga koji dodiruju te prave i prolaze kroz centar datog kruga, onda ćemo dobiti dva centra 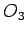 i
i 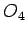 . Krugovi istih centara, sa poluprečnicima povećanim za poluprečnik datog kruga, dodiruju date prave
. Krugovi istih centara, sa poluprečnicima povećanim za poluprečnik datog kruga, dodiruju date prave  i
i  i dati krug
i dati krug  ali unutrašnjim dodirom.
ali unutrašnjim dodirom.
- Dokaz: Tačnost konstrukcije kruga koji dodiruje dve date prave i prolazi kroz datu tačku bila je potvrđena u zadatku 4. Za dokaz tačnosti konstrukcije krugova u ovom zadatku dovoljno je navesti dve osobine krugiva:
- ako imamo krug O koji prolazi kroz centar
 datog kruga, onda posle smanjenja poluprečnika kruga O za dužinu poluprečnika kruga
datog kruga, onda posle smanjenja poluprečnika kruga O za dužinu poluprečnika kruga  , koncentični krug dodiruje krug
, koncentični krug dodiruje krug 
- ako imamo krug O koji dodiruje pravu

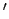 , onda posle smanjenja poluprečnika kruga O za dužinu rastojanja između paralelnih pravih
, onda posle smanjenja poluprečnika kruga O za dužinu rastojanja između paralelnih pravih  i
i 
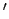 novi koncentrični krug će dodirivati pravu
novi koncentrični krug će dodirivati pravu  . Slične osobine krugova važe i za krugove čiji se poluprečnici povećavaju.
. Slične osobine krugova važe i za krugove čiji se poluprečnici povećavaju.
- Diskusija: U diskusiji ćemo se zaustaviti na navođenju nekoliko karakterističnih slučajeva, koji će u dovoljnoj meri dati sliku mogućih rešenja ovog zadatka.
- Ako dati krug
 ceo leži u uglu pravih
ceo leži u uglu pravih  i
i  , koji ćemo označiti sa
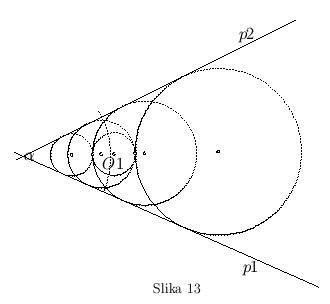
, koji ćemo označiti sa 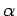 , onda navedene konstukcije daju četiri kruga, dva spoljašnjeg dodira i dva unurrašnjeg (sl. 13).
, onda navedene konstukcije daju četiri kruga, dva spoljašnjeg dodira i dva unurrašnjeg (sl. 13).
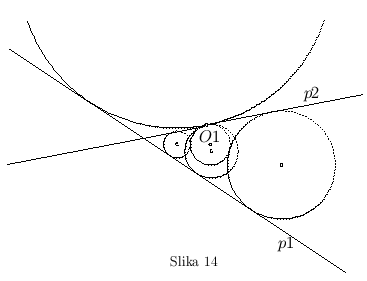
- Ako krug
 dodiruje pravu
dodiruje pravu  , a leži u uglu, vidi se da se krugovi sa unutrašnjim dodirom poklapaju. Pojavljuje se još jedan krug spoljašnjeg dodira za koji je prava
, a leži u uglu, vidi se da se krugovi sa unutrašnjim dodirom poklapaju. Pojavljuje se još jedan krug spoljašnjeg dodira za koji je prava  zajednička tangenta kruga
zajednička tangenta kruga  i tog novog dodirnog kruga (sl. 14).
i tog novog dodirnog kruga (sl. 14).
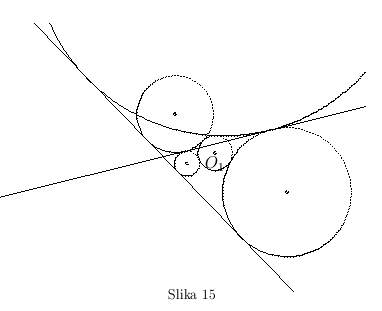
- Ako krug
 seče samo pravu
seče samo pravu  , krugovi unutrašnjeg dodira su nemogući, ali se umesto njih pojavljuju dva kruga spoljašnjeg dodira, znači ukupno četiri(sl. 15).
, krugovi unutrašnjeg dodira su nemogući, ali se umesto njih pojavljuju dva kruga spoljašnjeg dodira, znači ukupno četiri(sl. 15).
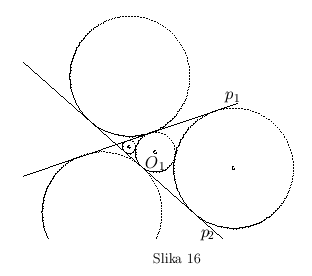
- Ako krug
 dodiruje obe date prave
dodiruje obe date prave  i
i  , tada se krug unutrašnjeg dodira degeneriše u dati krug
, tada se krug unutrašnjeg dodira degeneriše u dati krug  , ali se pojavljuju još dva kruga spoljašnjeg dodira (sl. 16).
, ali se pojavljuju još dva kruga spoljašnjeg dodira (sl. 16).
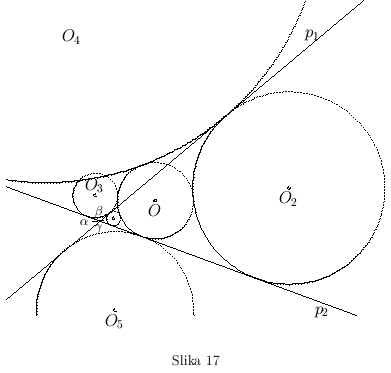
- Ako krug O seče neku pravu, recimo
 i dodiruje drugu, krugova unutrašnjeg dodira nema, ali ima pet krugova spoljašnjeg dodira: dva u uglu
i dodiruje drugu, krugova unutrašnjeg dodira nema, ali ima pet krugova spoljašnjeg dodira: dva u uglu 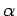 -
-  i
i 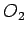 , dva u uglu
, dva u uglu 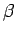 , gde se nalazi drugi deo datog kruga
, gde se nalazi drugi deo datog kruga  , i to
, i to 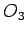 i
i 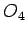 , i jedan u uglu
, i jedan u uglu 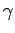 , suprotnom uglu
, suprotnom uglu 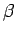 - krug
- krug 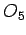 (sl. 17).
(sl. 17).
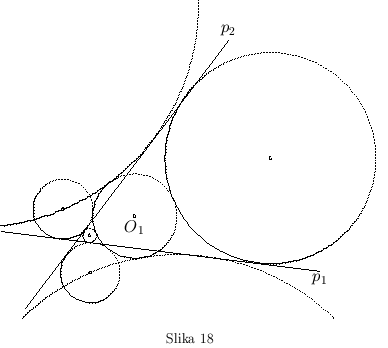
- Ako krug
 seče obe prave, ali se presečna tačka datih pravih nalazi van datog kruga, postoji šest krugova spoljašnjeg dodira (sl. 18).
seče obe prave, ali se presečna tačka datih pravih nalazi van datog kruga, postoji šest krugova spoljašnjeg dodira (sl. 18).
- Ako krug
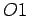 seče obe prave i presečna tačka pravih se nalazi u krugu, imamo četiri kruga unutrašnjeg dodira, i to po jedan krug u svakom od četiri ugla koji obrazuju te prave (sl. 19).
seče obe prave i presečna tačka pravih se nalazi u krugu, imamo četiri kruga unutrašnjeg dodira, i to po jedan krug u svakom od četiri ugla koji obrazuju te prave (sl. 19).
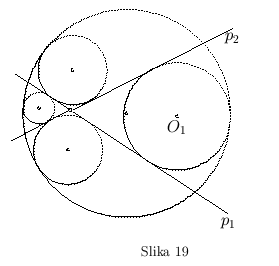
- Kao poslednji slučaj navedimo mogućnost kada krug
 prolazi kroz presečnu tačku pravih
prolazi kroz presečnu tačku pravih  i
i  i ne dodiruje nijednu od njih. U ovom slučaju imamo samo jedan krug unutrašnjeg dodira. Preostala tri kruga unutrašnjeg dodira degenerišu se u presečnu tačku datih pravih. Osim toga, imamo još tri kruga spoljašnjeg dodira (sl. 20).
i ne dodiruje nijednu od njih. U ovom slučaju imamo samo jedan krug unutrašnjeg dodira. Preostala tri kruga unutrašnjeg dodira degenerišu se u presečnu tačku datih pravih. Osim toga, imamo još tri kruga spoljašnjeg dodira (sl. 20).
2005-04-12
![]() i
i ![]() dve date prave i
dve date prave i ![]() dati krug (sl. 12).
dati krug (sl. 12).








