Neka su data dva kruga  i
i 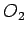 i tačka A. Treba kroz tačku A povući krug koji dodiruje ta dva kruga (sl. 22).
i tačka A. Treba kroz tačku A povući krug koji dodiruje ta dva kruga (sl. 22).
- Analiza: Pretpostavimo da je zadatak rešen i neka traženi krug O prolazi kroz tačku A i dodiruje krugove
 i
i 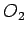 u tačkama
u tačkama 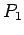 i
i 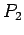 .
.
Konstruišimo pravu 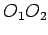 kroz centre datih krugova i spoljašnju tangentu
kroz centre datih krugova i spoljašnju tangentu 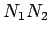 sa tačkama dodira
sa tačkama dodira 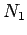 i
i 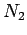 .Presečna tačka S prave
.Presečna tačka S prave 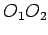 i tangente
i tangente 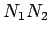 je centar sličnosti datih krugova.
je centar sličnosti datih krugova.
Tri tačke 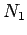 ,
, 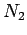 i A određuju krug koji prolazi kroz te tri tačke. Neka prava SA seče taj krug u tački B. Pošto su nam poznate četiri tačke toga kruga: A, B,
i A određuju krug koji prolazi kroz te tri tačke. Neka prava SA seče taj krug u tački B. Pošto su nam poznate četiri tačke toga kruga: A, B, 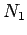 ,
, 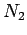 , imamo sledeću jednakost:
, imamo sledeću jednakost:
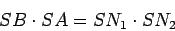 |
(2) |
Ova jednakost daje mogućnost određivanja položaja tačke B. Dalje važi:
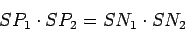 |
(3) |
jer za traženi krug O imamo:
U jednakosti (1) nepoznat je samo član SB, pa možemo konstruisati tu dužinu prema poznatom postupku za četvrtu proporcionalu. Tako je određena točka B kroz koju treba da prođe traženi krug.
Na taj način naš zadatak se svodi na konstruisanje kruga koji treba da prođe kroz dve tačke A i B i da dodiruje krug  . I tada postoji prava
. I tada postoji prava  O koja spaja centar
O koja spaja centar  datog kruga sa centrom O traženog kruga. Ta prava određuje tačku
datog kruga sa centrom O traženog kruga. Ta prava određuje tačku 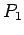 dodira krugova. Tačka
dodira krugova. Tačka 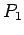 određuje dalje položaj prave
određuje dalje položaj prave 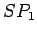 , koja određuje tačku
, koja određuje tačku 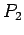 dodira kruga O sa drugim datom krugom
dodira kruga O sa drugim datom krugom 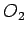 . Time se rešava dati zadatak7.
. Time se rešava dati zadatak7.
Na slici 22a tačka A i traženi krug O se nalazi van oblasti datih krugova  i
i 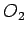 .
.
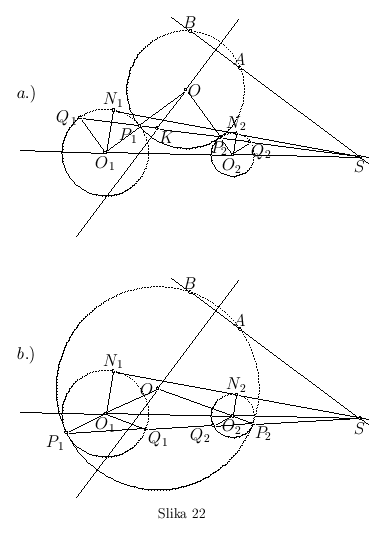
Na slici 22b imamo shemu slučaja kada traženi krug, prolazeći kroz datu tačku A, obuhvata date krugove.
- Konstrukcija: Konstrukciju ovog zadatka možemo podeliti u tri dela:
1. Konstrukcija tačke B kroz koju treba da prođe traženi krug.
2. Primena zadatka 3. o konstrukciji kruga koji prolazi kroz dve date tačke i dodiruje jedan od datih krugova.
3. Proširenje dodira na drugi krug.
- Dokaz: Elementi dokaza nalaze se u analizi.
- Diskusija: Diskusija ovog zadatka je vrlo opširna, pa je nećemo navoditi.
2005-04-12
![]() i
i ![]() i tačka A. Treba kroz tačku A povući krug koji dodiruje ta dva kruga (sl. 22).
i tačka A. Treba kroz tačku A povući krug koji dodiruje ta dva kruga (sl. 22).
