Neka su date tri prave  ,
,  ,
, 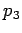 . Treba konstruisati krug koji dodiruje te tri prave.
. Treba konstruisati krug koji dodiruje te tri prave.
- Analiza: Ovaj zadatak formulisan rečima
'' U dati trougao upisati krug'' takođe se nalazi u IV knjizi, stav 4, Euklidovih '' Elemenata''.
Ovako glasi tekst ovog stava u prevodu:
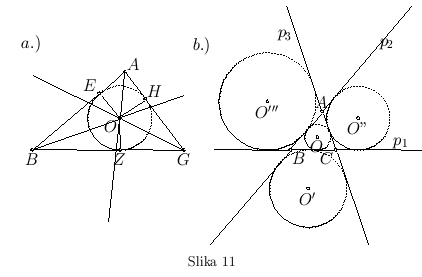
Neka je dat trougao 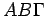 (sl. 11a). Treba u dati trougao upisati krug.
(sl. 11a). Treba u dati trougao upisati krug.
Prepolovimo uglove 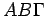 i
i 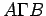 pravama
pravama 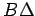 i
i 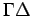 i neka se te prave seku u tački
i neka se te prave seku u tački 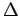 . Povucimo iz tačke
. Povucimo iz tačke 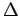 na prave AB,
na prave AB, 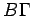 ,
, 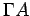 normale
normale 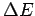 ,
, 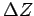 ,
, 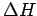 . Kako je ugao
. Kako je ugao 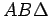 jednak uglu
jednak uglu
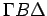 , a pravi ugao
, a pravi ugao 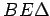 jednak pravom uglu
jednak pravom uglu 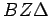 , dva trougla
, dva trougla 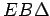 i
i 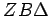 će imati po dva ugla jednaka i po jednu stranicu jednaku, i to stranicu
će imati po dva ugla jednaka i po jednu stranicu jednaku, i to stranicu 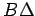 naspram jednakih uglova. Prema tome će i ostale stranice jednog trougla biti jednake ostalim stranicama drugog, tj.
naspram jednakih uglova. Prema tome će i ostale stranice jednog trougla biti jednake ostalim stranicama drugog, tj. 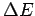 će biti jednako
će biti jednako 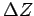 . Iz istih razloga i
. Iz istih razloga i 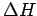 je jednako
je jednako 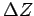 . To znači da su tri duži
. To znači da su tri duži 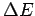 ,
, 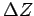 ,
, 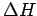 međusobno jednake. Prema tome krug sa centrom u
međusobno jednake. Prema tome krug sa centrom u 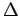 , opisan rastojanjem do jedne od tačaka E, Z, H kao poluprečnikom, će proći i kroz ostale tačke i u tačkama E, Z, H i dodirivati prave AB,
, opisan rastojanjem do jedne od tačaka E, Z, H kao poluprečnikom, će proći i kroz ostale tačke i u tačkama E, Z, H i dodirivati prave AB, 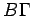 ,
, 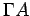 , jer su uglovi u tim tačkama pravi. Zaista, kad bi on sekao te prave, onda bi normala na prečnik, koja prolazi kroz njegov kraj, bila u krugu, a to je, kao što je dokazano, nemoguće. Prema tome, krug sa centrom u
, jer su uglovi u tim tačkama pravi. Zaista, kad bi on sekao te prave, onda bi normala na prečnik, koja prolazi kroz njegov kraj, bila u krugu, a to je, kao što je dokazano, nemoguće. Prema tome, krug sa centrom u 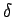 opisan rastojanjem do bilo koje od tačaka E, Z, H ne seče prave AB,
opisan rastojanjem do bilo koje od tačaka E, Z, H ne seče prave AB, 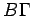 ,
, 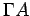 . Dakle, on ih dodiruje i biće krug upisan u trougao
. Dakle, on ih dodiruje i biće krug upisan u trougao 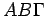 . Neka je on upisan kao ZHE.
Na ovaj način je u dati trougao
. Neka je on upisan kao ZHE.
Na ovaj način je u dati trougao 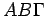 upisan krug EZH, a to je i trebalo izvesti.
upisan krug EZH, a to je i trebalo izvesti.
Analiza ovog zadatka može se izveti i nasledeći način:
Kako centar svakog kruga, koji dodiruje dve prave, mora da se nalazi na simetrali ugla između tih pravih, to se centar svakog kruga, koji dodiruje tri prave, mora nalaziti u preseku takvih simetrala, koje se sve tri seku u istoj odgovarajućoj tački Rri tom su uzete simetrale unutrašnjih ili spoljašnjih uglova. Tako ćemo dobiti, u opštem slučaju četiri kruga: krug sa centrom u O, upisan u trougao ABC (sl. 11b) i tri kruga sa centrima  ,
, 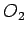 ,
,  , spolja dopisanih tom trouglu.
, spolja dopisanih tom trouglu.
- Konstrukcija: Konstruišemo simetrale
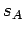 ,
,  ,
, 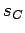 , uglova A, B, C i normale na te prave
, uglova A, B, C i normale na te prave  ,
, 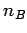 ,
, 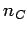 , koje su ustvari simetrale spoljašnjih uglova. Preseci pravih (
, koje su ustvari simetrale spoljašnjih uglova. Preseci pravih (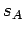 ,
, 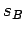 ,
, 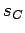 ), (
), (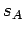 ,
, 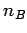 ,
, 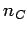 ), (
), ( ,
, 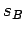 ,
, 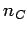 ), (
), ( ,
, 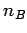 ,
, 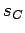 ) daju centre O - upisanog kruga i
) daju centre O - upisanog kruga i  ,
, 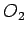 ,
, 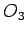 - spolja dopisanih krugova.
- spolja dopisanih krugova.
- Dokaz: Dokaz se zasniva na tome da se svaki centar nalazi na istom odstojanju od tri odgovarajuće prave.
- Diskusija: Treba proučiti sve moguće položaje pravih
 ,
,  ,
, 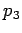 i u vezi sa tim položaje četiri gore navedena kruga.
i u vezi sa tim položaje četiri gore navedena kruga.
2005-04-12
![]() ,
, ![]() ,
, ![]() . Treba konstruisati krug koji dodiruje te tri prave.
. Treba konstruisati krug koji dodiruje te tri prave.
