Neka su date dve prave ![]() i
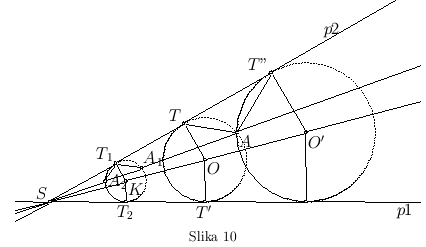
i ![]() i tačka A (sl. 10). Treba konstruisati krug koji dodiruje prave
i tačka A (sl. 10). Treba konstruisati krug koji dodiruje prave ![]() i
i ![]() i prolazi kroz tačku A.
i prolazi kroz tačku A.
1. seku se
2. paralelne su
3. poklapaju se
Tačka A može biti u jednom od položaja:
a) bilo gde u ravni osim na pravama ![]() i
i ![]()
b) na jednoj od pravih, sem tačke S, preseka pravih ![]() i
i ![]()
c) u tački S preseka pravih
Navedimo i rešenja pomenutih slučajeva. Slučajeve ćemo označavati tako da broj označava uslov za prave, a slovo za njim, uslov za tačku.
1.a) Dva kruga koja prolaze kroz tačku A i dodiruju prave ![]() i
i ![]() .
.
1.b) Dva kruga koja prolaze kroz tačku A na pravoj ![]() i dodiruju prave
i dodiruju prave ![]() i
i ![]()
1.c) Krug degeneriše u tačku A
2.a) Dva kruga
2.b) Jedan krug
2.c) Slučaj je nemoguć
3.a) Dva sistema krugova sa jedne strane dvostruke prave
3.b) Dva sistema krugova
3.c) Krug degeneriše u tačku A
2005-04-12