Diskusija: Pošto su osnovni geometrijski objekti u našem zadatku:
1. dati krug  datog poluprečnika R,
datog poluprečnika R,
2. dve tačke A i B kroz koje treba da prođe traženi krug,
tada u diskusiji treba da se prouče moguće promene svakog od tih objekata i, pored toga
3. da se ispita relativni položaj kruga prema tačkama A i B, a to znači i prema pravoj koja prolazi kroz ove dve tačke.
Krug, sam po sebi, određuje se samo jednim svojim parametrom, tzv. parametrom veličine: poluprečnikom R, koji može uzimati sve pozitivne vrednosti od 0 do 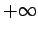 . Za prvu krajnju vrednost krug se pretvara u tačku i naš zadatak se degeneriše u prvi zadatak ovoga rada, kada traženi krug dodiruje tri date tačke. U drugom slučaju, kada
. Za prvu krajnju vrednost krug se pretvara u tačku i naš zadatak se degeneriše u prvi zadatak ovoga rada, kada traženi krug dodiruje tri date tačke. U drugom slučaju, kada
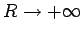 , krug se degeneriše u pravu, a naš zadatak se pretvara u zadatak o krugu koji prolazi kroz dve date tačke A i B i dodiruje pravu, koja je nastala od kruga, u ovom slučaju.
, krug se degeneriše u pravu, a naš zadatak se pretvara u zadatak o krugu koji prolazi kroz dve date tačke A i B i dodiruje pravu, koja je nastala od kruga, u ovom slučaju.
Drugi geometrijski objekat čine dve tačke A i B. Kao parametar veličine tog geometrijskog objekta služi rastojanje između tih tačaka, AB=2b.1.6 Pri b = 0 tačke se poklapaju, a pri
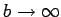 , jedna ili obe tačke odlaze u beskonačnost, a sredina - tačka P, može da ostane na mestu. Ako tačke A i B imaju određeni konačni položaj i prava AB ima određeni pravac, onda određeni položaj ima i simetrala tačaka A i B, tj. prava normalna na pravu AB, koja prolazi kroz tačku P. U teoriji krugova ta simetrala igra veoma važnu ulogu, jer centar svakog kruga koji prolazi kroz dve tačke A i B mora da se nalazi na simetrali duži određene tim tačkama.
, jedna ili obe tačke odlaze u beskonačnost, a sredina - tačka P, može da ostane na mestu. Ako tačke A i B imaju određeni konačni položaj i prava AB ima određeni pravac, onda određeni položaj ima i simetrala tačaka A i B, tj. prava normalna na pravu AB, koja prolazi kroz tačku P. U teoriji krugova ta simetrala igra veoma važnu ulogu, jer centar svakog kruga koji prolazi kroz dve tačke A i B mora da se nalazi na simetrali duži određene tim tačkama.
Pri proučavanju mogućih položaja tačaka A i B prema datom krugu  mogu se razlikovati sledeći slučajevi4:
mogu se razlikovati sledeći slučajevi4:
- Tačke A i B su van kruga
 .
.
- Jedna od tačaka je na krugu, a druga van kruga.
- Jedna od tačaka je na krugu, a druga u krugu.
- Obe tačke su u krugu.
Za proučavanje različitih položaja tačaka A i B prema datom krugu  , zgodno je uzeti u obzir pravu koja prolazi kroz tačke A i B.
Ta prava može:
, zgodno je uzeti u obzir pravu koja prolazi kroz tačke A i B.
Ta prava može:
1. biti van kruga,
2. dodirivati krug,
3. seći krug.
Diskusija svih mogućih slučajeva ne zadaje teškoće, ali zahteva veliku pažnju.
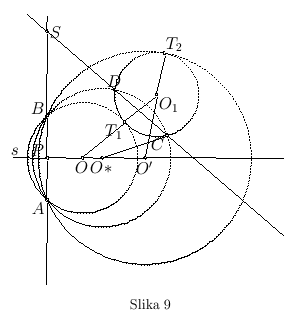
![]() (sl. 9). Treba kroz A i B konstruisati krug koji dodiruje dati krug
(sl. 9). Treba kroz A i B konstruisati krug koji dodiruje dati krug ![]() .
.