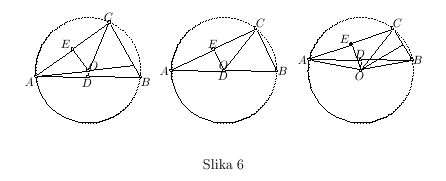
Prepolovimo prave AB, AC tačkama D i E i kroz njih povučemo prave DO i EO pod pravim uglovima prema pravama AB i AC. One se seku ili u trouglu ABC ili na pravoj AB ili sa druge strane prave AB, van trougla ABC. Presečna tačka O je centar kruga koji prolazi kroz tačke A, B, C.
a) Neka je prvo O u trouglu, pa povucimo OB, OC i OA. Tada, pošto je AD jednako DB, a DO zajedničko i upravno na AB, stranica AO jednaka je stranici OB. Na sličan način se dokazuje da je CO jednako AO, pa je prema tome OB jednako OC. Dakle duži OA, OB, OC su međusobno jednake. Prema tome krug sa centrom u O opisan rastojanjem do jedne od tačaka A, B, C će proći i kroz ostale tačke i biće krug opisan oko trougla ABC.
b) Uzmimo sad da se DO i EO seku na pravoj AB u tački O, pa povucimo CO. Na sličan način se dokazuje da će tačka O biti centar kruga opisanog oko trougla ABC.
c) Najzad, neka se DO i EO seku u tački O van trougla ABC, pa povucimo AO, BO i CO. Kako je opet AD jednako DB, a DO je zajednička stranica upravna na AB, stranica AO jednaka je stranici BO. Na sličan način se dokazuje da je CO jednako AO, prema tome je i BO jednako OC. Dakle, opet će krug sa centrom u O opisan rastojanjem do jedne od tačaka A, B, C proći i kroz ostale tačke i biti opisan oko trougla ABC. Na ovaj način oko datog trougla je opisan krug, a to je i trebalo dokazati.
Svoje izlaganje Euklid je dopunio, u obliku ''Posledice'', analizom vrednosti uglova za različite položaje centra opisanog kruga. Njegovi rezultati su formulisani ovako:
- ako se ugao ACB nalazi u kružnom odsečku većem od polukruga, taj ugao je manji od pravog
- ako je odsečak jednak polukrugu, ugao je jednak pravom
- ako je odsečak manji od polukruga, ugao je veći od pravog