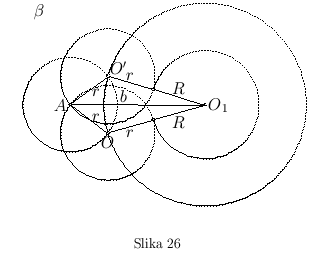
Neka je dat krug ![]() poluprečnika R i tačka A. Treba kroz tačku A povući krug datog poluprečnika r, tako da on dodiruje krug
poluprečnika R i tačka A. Treba kroz tačku A povući krug datog poluprečnika r, tako da on dodiruje krug ![]() (sl. 26).
(sl. 26).
| USLOVI | SLUČAJ | REŠENJE | ||
| 1.1.1 | nema rešenja | |||
| 1.1.2 | jedno rešenje | |||
| 1.3 | dva spoljašnja kruga | |||
| 1.3.1 | dva spoljašnja i jedan | |||
| unutrašnji dodir | ||||
| 1.3.2 | dva spoljašnja i dva | |||
| unutrašnja dodira | ||||
| 1.2.1 | nema rešenja | |||
| 1.2.2 | jedno rešenje | |||
| 1.2.3 | dva spoljašnja kruga | |||
| 1.3.1 | nema rešenja | |||
| 1.3.2 | jedno rešenje | |||
| 1.3.3 | dva spoljašnja kruga | |||
| 2.1 | jedan krug spoljašnjeg | |||
| dodira | ||||
| 2.2 | jedan krug spoljašnjeg | |||
| dodira, drugi krug se | ||||
| poklapa sa datim | ||||
| krugom | ||||
| 2.3 | jedan krug spoljašnjeg | |||
| dodira i jedan krug | ||||
| unutrašnjeg dodira, koji | ||||
| je obuhvaćen datim krugom | ||||
| 3.1 | slučaj je nemoguć | |||
| 3.2 | slučaj je nemoguć | |||
|
|
3.3.1 | dva rešenja | ||
|
|
3.3.2 | dva rešenja; izuzetan slučaj: | ||
| 3.3.2.1 | postoji beskonačno mnogo | |||
| rešenja | ||||
|
|
3.3.3.1 | dva rešenja | ||
| 3.3.3.2 | jedno rešenje | |||
| 3.3.3.3 | nema rešenja |
Ovi rezultati pokazuju da u relativno jednostavnom zadatku, kao što je ovaj, diskusija može biti prilično opširna, zbog većeg broja parametara. Takođe, iz diskusije ovog zadatka se vidi da i sama konstrukcija, koja kako u početku izgleda, rešava zadatak u potpunosti, može biti nedovoljna i mora biti proširena na razne slučajeve diskusije.