-
- 1
- Euklidovi elementi, O dodiru dva kruga, 26-29 teoreme, Klasični naučni spisi MI SANU, knj. III, Beograd 1953.
- 2
- Quaestiones Archimedeae, Hauniae, 1879, S. 29. O dodiru krugova Arhimed je napisao specijalnu raspravu, koju je obredio T. L. Heiberg.
- 3
- Rad Apolonija
 - prema Paposu je izgubljen. Pappos-ed. Hultsch II, S. 647.
- prema Paposu je izgubljen. Pappos-ed. Hultsch II, S. 647.
- 4
- Vi
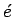 te: Apollonius Gallus, Paris 1600, Viete, Opera, S. 325-346.
te: Apollonius Gallus, Paris 1600, Viete, Opera, S. 325-346.
- 5
- Papos: četvrta knjiga zbornika
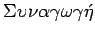 Pappous, N. 15, ed Hultsch, I str. 200.
Pappous, N. 15, ed Hultsch, I str. 200.
- 6
- E. Koetter: Die Entwicklung der synthetischen Geometrie, Jahresber. d. Dtsch. Math. Verein. 5, II, Leipzig 1901. S. 109 ff.
- 7
- J. A. Grunert (1834): Lehrbuch der Math. f. mittl. Klasse, II, Ebene Geometrie, 404-407.
- 8
- A. L. Crelle (1826): Elemente. I. 1826, § 290 und 399 Gauss, Werke 4. Gött. 1880, S. 399 f.
- 9
- Herm. Bodenstedt (1906): Geometrografische Losungen der zehn Hauptfalle. ... Das Berührungssystem des Apollonius. Z. math. nat. Unt. 37, 1906, S. 89-102
- 10
- Genauere Geschichte vgl. W. Killing und H. Hovestadt- Handbuoh des mathemathischen Unterrichts. B. 1. 1901. S. 414 ff. 24
- 11
- H. Thieme: Die Elemente der Geometrie. Leipzig und Berlin. 1909. Ed 13. S. Teubner.
- 12
- M. Zacharias: Encykl. d. math. Wiss. III. AB 9. Leipzig 1921. S. 1102-1103.
iso88595
- 13
- Э. Котъмaн: История математики в древности. Москва, 1961. г.
- 14
- А. П. Юшкевич: История математики в средние века. Москва, 1961. г.
2005-04-12