Neka su data dva kruga  i
i 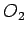 , poluprečnika
, poluprečnika 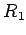 i
i 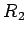 (
(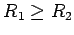 ) i prava
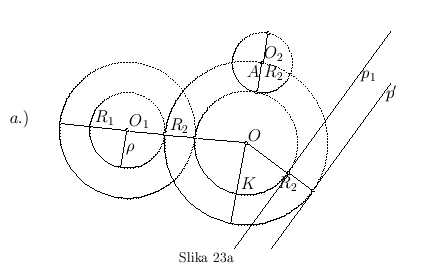
) i prava  . Treba konstruisati krug koji dodiruje krugove
. Treba konstruisati krug koji dodiruje krugove  ,
, 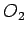 i pravu
i pravu  (sl. 23a).
(sl. 23a).
- Analiza: Ako povučemo pravu
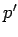 paralelnu pravoj
paralelnu pravoj  na rastojanju
na rastojanju 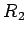 sa suprotne strane od one na kojoj su krugovi
sa suprotne strane od one na kojoj su krugovi  i
i 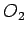 , tada se naš zadatak svodi na konstrukciju kruga koji prolazi kroz tačku
, tada se naš zadatak svodi na konstrukciju kruga koji prolazi kroz tačku 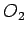 , dodiruje pravu
, dodiruje pravu 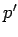 i krug poluprečnika
i krug poluprečnika
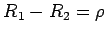 .
.
- Konstrukcija: Konstruišimo pravu
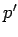 , paralelnu pravoj p na rastojanju
, paralelnu pravoj p na rastojanju 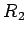 i to sa druge strane od one na kojoj su dati krugovi. Smanjimo poluprečnike krugova
i to sa druge strane od one na kojoj su dati krugovi. Smanjimo poluprečnike krugova  i
i 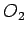 za dužinu
za dužinu 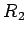 . Tada, od prvog kruga
. Tada, od prvog kruga  ostaje krug poluprečnika
ostaje krug poluprečnika 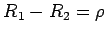 , a od drugog samo centar, koji kao tačku označimo sa A. Posle izvršene ove konstrukcije, naš zadatak se svodi na konstrukciju kruga O, koji treba da dodiruje krug poluprečnika
, a od drugog samo centar, koji kao tačku označimo sa A. Posle izvršene ove konstrukcije, naš zadatak se svodi na konstrukciju kruga O, koji treba da dodiruje krug poluprečnika 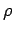 i pravu
i pravu 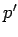 koja prolazi kroz tačku A, a to je zadatak 7. Ako kao rešenje ovog problema dobijemo krug određenog položaja i nekog poluprečnika
koja prolazi kroz tačku A, a to je zadatak 7. Ako kao rešenje ovog problema dobijemo krug određenog položaja i nekog poluprečnika 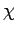 , onda je odgovor na dati zadatak koncentrični krug poluprečnika
, onda je odgovor na dati zadatak koncentrični krug poluprečnika 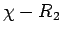 .
.
- Dokaz: Dokaz je jasan iz analize i zadatka 7.
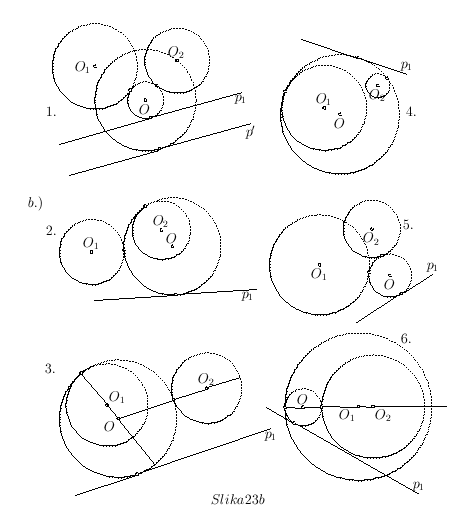
- Diskusija: Diskusija ovog zadatka je vrlo opširna, pa ćemo pokazati samo nekoliko slika (sl. 23b) za jedan konkretan slučaj, koje daju predstavu o karakteru rešenja.
2005-04-12
![]() i
i ![]() , poluprečnika
, poluprečnika ![]() i
i ![]() (
(![]() ) i prava
) i prava ![]() . Treba konstruisati krug koji dodiruje krugove
. Treba konstruisati krug koji dodiruje krugove ![]() ,
, ![]() i pravu
i pravu ![]() (sl. 23a).
(sl. 23a).

