Ako je neka duž podeljena neprekidno, pa joj se doda veći deo podeljene duži, biće i cela dobivena duž podeljena neprekidno i njen veći deo je polazna duž.

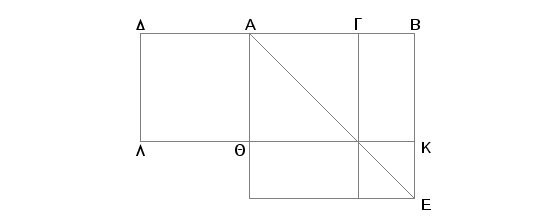
Neka je duž AB podeljena tačkom G neprekidno i neka je veći deo AG. Odmerimo AD jednako AG. Tvrdim da se duž DB deli tačkom A neprekidno i da je veći deo polazna duž AB.
Zaista, konstruišimo na AB kvadrat AE i nacrtajmo sliku. Pošto je AB podeljeno tačkom G neprekidno, biće pravougaonik obuhvaćen od AB i BG jednak kvadratu od AG [VI, Def. 3, VI.17]. Ali pravougaonik obuhvaćen od AB i BG je GE, a kvadrat na AG je GQ. Prema tome je GE jednako QG. No GE je jednako QE, a QG - DQ. Na taj način DQ je jednako QE [a dodajemo isto QB]. Prema tome je celo DK jednako celom AE. No DK je pravougaonik obuhvaćen od BD i DA jednak kvadratu na AB. A otuda sleduje da je DB prema BA kao BA prema AD [VI.17]. Kako je DB veće od BA, biće i BA veće od AD [V.14].
Na taj način tačka A deli DB neprekidno i veći deo je AB. A to je trebalo dokazati.