15.

Konstruisati kocku, obuhvatiti je sferom, kao i piramidu, i dokazati da je kvadrat na prečniku sfere triput veći od kvadrata na ivici kocke.

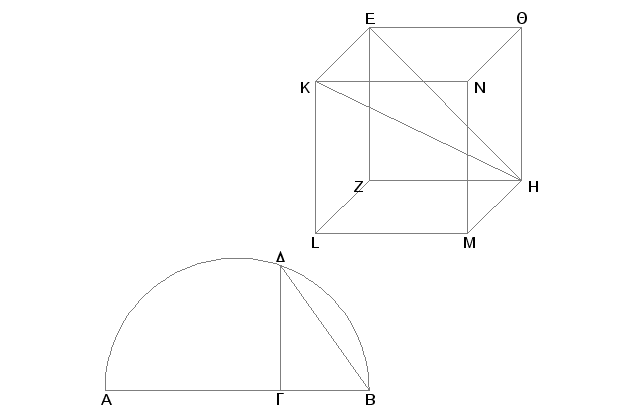
Odmerimo AB kao prečnik date sfere i podelimo ga tačkom G tako da AG bude dvaput veće od BG. Dalje, nacrtajmo na AB polukrug ADB, iz G podignimo normalu GD na AB, povucimo DB, konstruišimo kvadrat EZHQ kome je strana jednaka DB. Pa kroz tačke E, Z, H, Q u ravni kvadrata EZHQ povucimo normale EK, ZL, HM, QN, odmerimo na svakoj od EK, ZL, HM, QN duži EK, ZL, HM, QN od kojih je svaka jednaka jednoj od duži EZ, ZH, HQ, QE i spojimo K sa L, L sa M, M sa N, N sa K. Tako je načinjena kocka ZN obuhvaćena sa šest jednakih kvadrata.
Treba je obuhvatiti datom sferom i dokazati da je kvadrat na prečniku sfere triput veći od kvadrata na ivici kocke.
Zaista, nacrtajmo KH i EH. I pošto je ugao KEH prav, jer je KE normala na ravni EH, dakle i na pravoj EH [XI, Def. 3], to će polukrug konstruisan na KH proći i kroz tačku E. Zatim pošto je HZ normalno prema svakom od ZL i ZE, biće i HZ normalno i prema ravni ZK; prema tome, ako konstruišemo ZK, biće HZ normalno i prema ZK. I iz istih razloga, ponovo, polukrug konstruisan na HK proći će i kroz tačku Z. A proći će slično i kroz preostale tačke kocke. Ako se, pri nepokretnom KH, polukrug okrene i ponovo vrati u početni položaj, biće kocka obuhvaćena sferom. Tvrdim da je to data sfera. Zaista, pošto je HZ jednako ZE i ugao kod tačke Z je prav, biće kvadrat na EH dvaput veći od kvadrata na EZ. No EZ je jednako EK. Znači, kvadrat na EH je dvaput veći od kvadrata na EK, a zbir kvadrata na EH i na EK, tj. kvadrat na HK [I.47], je triput veći od kvadrata na EK. I pošto je AB triput veće od GB i AB je prema BG kao kvadrat na AB prema kvadratu na BD, biće kvadrat na AB triput veći od kvadrata na BD. A dokazano je da je i kvadrat na HK triput veći od kvadrata na KE. I KE je uzeto jednako DB. Pa prema tome je i KH jednako AB. A kako je AB jednako prečniku date sfere, biće i KH jednako prečniku date sfere.
Na ovaj način, kocka je obuhvaćena datom sferom. I u isto vreme, dokazano je da je kvadrat na prečniku sfere triput veći od kvadrata na ivici kocke. A to je trebalo dokazati.