Ako su dve prave upravne na istoj ravni, one su paralelne.

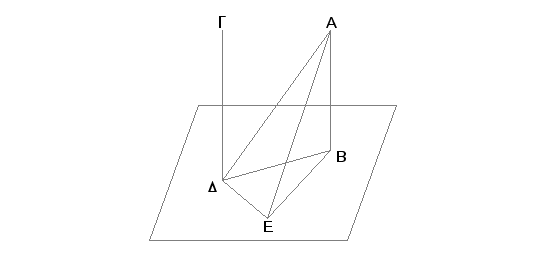
Zaista, neka prave AB i GD stoje pod pravim uglovima prema osnovnoj ravni. Tvrdim da je prava AB paralelna sa pravom GD.
Zaista, neka one seku osnovnu ravan u tačkama B i D, pa povucimo pravu BD i neka je DE prava u osnovnoj ravni upravna na BD; dalje odmerimo DE jednako AB i povucimo BE, AE, AD. Pošto je duž AB normalna na osnovnoj ravni, ona će obrazovati prav ugao sa svakom pravom koja je seče i nalazi se u osnovnoj ravni [XI, Def. 3]. No AB seče svaku od pravih BD i BE, koje se nalaze u osnovnoj ravni. Prema tome je svaki od uglova ABD i ABE prav. Iz istih razloga je svaki od uglova GDB i GDE prav. I pošto je AB jednako DE, a BD je zajednička, dve strane AB, BD jednake su dvema stranama ED, DB. I one obrazuju prave uglove. Tada je osnovica AD jednaka osnovici BE [I.4]. I pošto je AB jednako DE, a i AD jednako BE, znači dve strane AB, BE jednake su dvema stranama ED, DA, a i osnovica AE im je zajednička. Prema tome je ugao ABE jednak uglu EDA [I.8]. A kako je ugao ABE prav, biće prav i ugao EDA. Znači ED je upravna na DA. Dakle, ona je upravna i prema svakoj od BD i DG. Prema tome je ED upravna na tri prave BD, DA i DG, koje imaju sa njom zajedničku tačku. Zbog toga se tri prave BD, DA i DG nalaze u istoj ravni [XI.5]. I u onoj ravni u kojoj se nalaze DB i DA, nalazi se i AB, jer se ceo trougao nalazi u istoj ravni [XI.2]. Prema tome su prave AB, BD i DG u istoj ravni. I svaki je od uglova ABD i BDG prav, te je AB paralelna sa GD [I.28].
Na ovaj način, ako su dve prave upravne na istoj ravni, one su paralelne. A to je trebalo dokazati.