Prava povučena kroz presečnu tačku dve prave pod pravim uglovima prema svakoj od njih biće pod pravim uglom i prema ravni tih pravih.

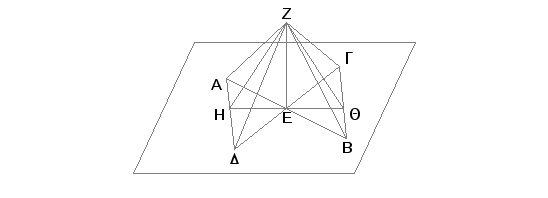
Zaista, neka je prava EZ, koja prolazi kroz presečnu tačku E pravih AB i GD, pod pravim uglovima prema tim pravima. Tvrdim, da je EZ pod pravim uglom i prema ravni pravih AB i GD.
Zaista, odmerimo među sobom jednake duži AE, EB, GE, ED i kroz E povucimo proizvoljnu pravu HEQ, nacrtajmo AD i GB i zatim kroz tačku Z povucimo duži ZA, ZH, ZD, ZG, ZQ, ZB. Pošto su dve duži AE i ED jednake dvema dužima GE i EB i one čine jednake uglove [I.15], onda je osnova AD jednaka osnovi GB i trougao AED jednak trouglu GEB [I.4]. Usled toga je i ugao DAE jednak uglu EBG. Ali i ugao AEH je jednak uglu BEQ [I.15]. Prema tome imamo dva trougla AHE i BEQ, kod kojih su dva ugla jednog jednaka sa dva odnosna ugla drugog, svaki-svakom; i jedna strana AE između uglova jednog je jednaka odgovarajućoj strani EB drugog. Oni tada imaju i ostale strane jednake ostalim stranama [I.26]. Na ovaj način je HE jednako EQ i AH jednako BQ. I pošto je AE jednako EB, a ZE zajednička strana pri pravim uglovima, onda je osnova ZA jednaka osnovi ZB [I.4]. Iz istih razloga je ZG jednako ZD. I pošto je AD jednako GB i ZA jednako ZB, znači dve strane ZA i AD jednake dvema stranama ZB i BG, svaka svakoj, a dokazano je da je i osnovica ZD jednaka osnovici ZG, biće jednaki i uglovi ZAD i ZBG [I.8]. I pošto je još dokazano da je AH jednako BQ, a i ZA da je jednako ZB, onda su dve strane ZA i AH jednake dvema stranama ZB i BQ; a takođe je dokazano da je ugao ZAH jednak uglu ZBQ. Otud zaključujemo da je i osnovica ZH jednaka osnovici ZQ [I.4]. I pošto je još, prema dokazanom, HE jednako EQ, a EZ je zajednička strana, znači dve strane HE, EZ jednake su dvema stranama QE i EZ, a osnovica ZH jednaka je osnovici ZQ, pa prema tome i ugao HEZ jednak je uglu QEZ [I.8]. Na taj način je svaki od uglova HEZ i QEZ prav. Prema tome je ZE upravna na proizvoljnoj pravoj kroz tačku E. Na sličan način se dokazuje da ZE čini prav ugao sa svakom pravom koja je seče i nalazi se u osnovnoj ravni. No prava je upravna na ravni, ako čini prav ugao sa svakom pravom koja je seče i nalazi se u toj ravni [XI, Def. 3]. Prema tome je prava ZE upravna na osnovnoj ravni. Ali osnovna ravan je ravan pravih AB i GD. Prema tome je ZE pod pravim uglom prema ravni pravih AB i GD.
Na ovaj način, prava povučena kroz presečnu tačku dve prave pod pravim uglovima prema svakoj od njih biće pod pravim uglom i prema ravni tih pravih. A to je trebalo dokazati.