38.

Ako su ivice naspramnih strana kocke (kuba) prepolovljene i kroz deone tačke povučene ravni, zajednički presek tih ravni i dijagonala kocke se polove.

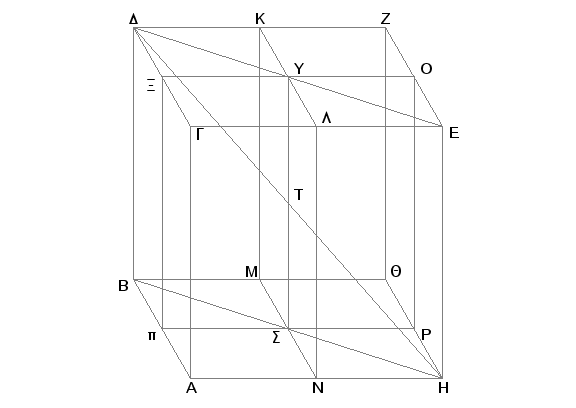
Zaista, neka su ivice naspramnih strana GZ i AQ kocke LZ prepolovljene tačkama K, L, M, N, X, p, O, P, kroz preseke konstruisane ravni KN i XP, čiji je zajednički presek YS, i DH dijagonala kocke. Tvrdim da su jednake duži: YT sa TS i DT sa TH.
Zaista, spojimo DY, YE, BS i SH. Pošto je DX paralelno sa OE, biće unakrsni uglovi DXY i YOE jednaki među sobom [I.29]. I pošto je DX jednako OE i XY jednako YO i obuhvataju jednake uglove, biće osnovica DY jednaka YE, trougao DXY jednak trouglu OYE, a ostali uglovi jednaki ostalim uglovima [I.4]. Prema tome je ugao XYD jednak uglu OYE. Zbog toga je DYE prava linija [I.14]. Iz istih razloga je i BSH prava linija i BS jednako SH. I pošto je GA jednako i paralelno sa DB, a GA je jednako i paralelno i sa EH, biće DB jednako i paralelno sa EH [XI.9]. A spajaju ih duži DE i BH. Prema tome su paralelne i duži DE i BH [I.33]. Zbog toga je ugao EDT jednak uglu BHT, jer su unakrsni [I.29], a i ugao DTY jednak je uglu HTS [I.15]. Postoje dva trougla DTY, HTS, koji imaju dva ugla jednaka sa dva ugla i jednu stranu jednaku jednoj strani, spram jednakih uglova, tj. DY i HS, jer su polovine duži DE i BH. Stoga su i ostale strane jednake ostalim stranama [I.26]. Prema tome je DT jednako HT i YT jednako TS.
Na ovaj način, ako su ivice naspramnih strana kocke (kuba) prepolovljene i kroz deone tačke povučene ravni, zajednički presek tih ravni i dijagonala kocke se polove. A to je trebalo dokazati.