36.
Ako su tri duži (neprekidno) proporcionalne, biće zapremina paralelepipeda sastavljenog od njih (kao ivica) jednaka zapremini jednakoivičnog paralelepipeda, sastavljenog od srednje duži sa uglovima jednakim uglovima polaznog (paralelepipeda).
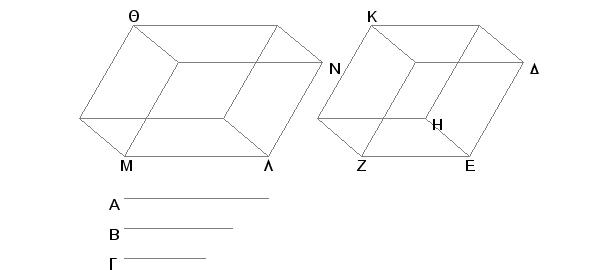
Neka su A, B, G tri (neprekidno) proporcionalne duži, tj. neka je A prema B kao B prema G. Tvrdim, da je zapremina paralelepipeda sa ivicama A, B, G jednaka zapremini jednakoivičnog paralelepipeda sa ivicom B i sa uglovima jednakim uglovima prvog paralelepipeda.
Konstruišimo kod tačke E rogalj obuhvaćen sa DEH, HEZ i ZED, odmerimo DE, HE, EZ svaku jednaku duži B i dopunimo paralelepiped EK. Odmerimo zatim LM jednako A, konstruišimo na duži LM, kod tačke L, rogalj jednak roglju kod tačke E, obuhvaćen uglovima NLX, XLM i MLN i odmerimo LX jednako B i LN jednako G. Pošto je A prema B kao B prema G, a A je jednako LM, B svakom od LX i ED, i G jednako LN, biće LM prema EZ kao DE prema LN. A kod jednakih uglova NLM i DEZ kraci su obrnuto proporcionalni, prema tome je paralelogram MN jednak paralelogramu DZ [VI.14]. I pošto su dva ravna pravolinijska ugla DEZ i NLM jednaka i nad njima su konstruisane jedna drugoj jednake duži LX i EH, koje sa polaznim pravima obrazuju jednake uglove, svaki svakom, biće jednake među sobom i normale spuštene iz tačaka H i X na ravni kroz NLM i kroz DEZ [XI.35, Posledica]. Prema tome su tela LQ i EK, svako, iste visine. A paralelepipedi sa jednakim osnovama i istim visinama jednaki su među sobom [XI.31]. Zbog toga je telo QL jednako telu EK. A telo LQ sastavljeno od A, B, G, a telo EK od B.
Na ovaj način, zapremina paralelepipeda sastavljenog od A, B, G jednaka je zapremini jednakoivičnog paralelepipeda sastavljenog od B, sa uglovima jednakim uglovima prvog paralelepipeda. A to je trebalo dokazati.