35.

Ako su data dva jednaka ravna ugla i kroz njihova temena povučene, iznad ravni tih uglova, prave, koje koje obrazuju jednake uglove sa kracima uglova, svaka sa svakim, pa se na povučenim pravima uzmu proizvoljne tačke i iz njih spuste normale na ravni polaznih uglova, i podnožja tih normala spoje sa temenima polaznih uglova, biće uglovi između tih spojnica i van ravni povučenih pravih jednaki među sobom.

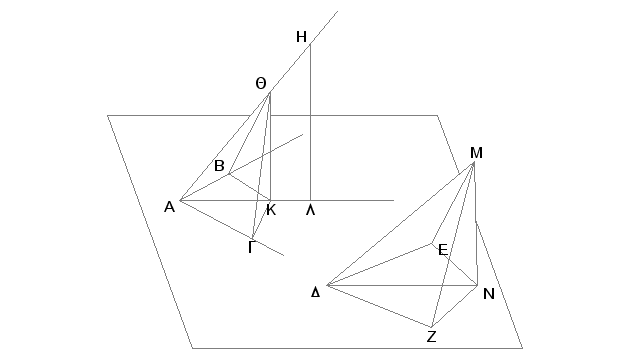
Neka su BAG i EDZ dva pravolinijska ugla i AH i DM iz tačaka A i D povučene van ravni tih uglova prave, koje obrazuju jednake uglove sa kracima polaznih uglova, svaka sa svakim, ugao MDE jednak je uglu HAB i ugao MDZ - uglu HAG;neka su na pravima AH i DM uzete proizvoljne tačke H i M, iz tačaka H i M, spuštene normale na ravni kroz BAG i kroz EDZ, neka su tačke N i L podnožja normala MN i HL na tim ravnima i povučene spojnice LA i ND. Tvrdim da je ugao HAL jednak uglu MDN.
Uzmimo AQ jednako DM i povucimo kroz tačku Q pravu QK paralelnu HL. Pošto je HL normalna na ravni kroz BAG, biće i QK normalna na ravni kroz BAG [XI.8]. Povucimo iz tačaka K i N normale KG, NZ, KB, NE na prave AG, DZ, AB, DE i uzmimo spojnice QG, GB, MZ, ZE. Pošto je kvadrat na QA jednak zbiru kvadrata na QK i KA, a kvadrat na KA jednak zbiru kvadrata na KG i na GA [I.47], biće kvadrat na QA jednak zbiru kvadrata na QK, na KG i na GA. A pošto je zbir kvadrata na QK i na KG jednak kvadratu na QG [I.47], biće kvadrat na QA jednak zbiru kvadrata na QG i na GA. Prema tome je ugao QGA prav [I.48]. Iz istih razloga i ugao DZM je prav. Dakle, ugao QAG jednak je uglu MDZ. Postoje dva trougla MDZ i QAG, koji imaju po dva jednaka ugla, svaki svakom, i po jednu jednaku stranu, QA jednaku MD, spram jednakih uglova. Prema tome su i ostale strane jednake ostalim stranama [I.26]. Znači i AG jednaka je DZ. Slično se dokazuje da je i AB jednaka DE [i to ovako: spojimo QB i ME. Pošto je kvadrat na AQ jednak zbiru kvadrata na AK i na KQ, a kvadrat na AK jednak zbiru kvadrata na AB i na BK, biće zbir kvadrata na AB, na BK i na KQ jednak kvadratu na AQ. Ali zbir kvadrata na BK i KQ jednak je kvadratu na BQ, jer je ugao QKB prav, kao ugao normale na osnovnoj ravni. Prema tome je kvadrat na AQ jednak zbiru kvadrata na AB i BQ. Znači ugao ABQ je prav. Iz istih razloga i ugao DEM je prav. A i ugao BAQ jednak je uglu EDM po pretpostavci, i AQ je jednako DM, znači i AB je jednako DE]. Pošto je sad AG jednako DZ i AB jednako DE, dve duži GA i AB jednake su dvema dužima ZD i DE, a i ugao GAB jednak je uglu ZDE, biće osnovica BG jednaka osnovici EZ, trougao - trouglu i ostali uglovi ostalim uglovima [I.4], te prema tome je i ugao AGB jednak uglu DZE. A takođe je i prav ugao AGK jednak pravom uglu DZN. Dakle i preostali ugao BGK jednak je preostalom uglu EZN. Iz istih razloga i ugao GBK jednak je uglu ZEN. Postoje dva trougla BGK i EZN, koji imaju po dva jednaka ugla, svaki svakom i po jednu jednaku stranu BG i EZ spram jednakih uglova, prema tome su i ostale strane jednake ostalim stranama [I.26]. Znači da je GK jednako ZN. A i AG jednako DZ. Dve duži AG i GK jednake su dvema dužima DZ i ZN i čine prave uglove. Prema tome i osnovica AK jednaka je osnovici DN [I.4]. I pošto je AQ jednako DM, biće jednak i kvadrat na AQ kvadratu na DM. Ali kvadrat na AQ jednak je zbiru kvadrata na AK i na KQ, jer je ugao AKQ prav [I.47]. I kvadrat na DM jednak je zbiru kvadrata na DN i na NM, jer je ugao DNM prav [I.47]. Na taj način zbir kvadrata na AK i na KQ jednak je zbiru kvadrata na DN i NM, od kojih je kvadrat na AK jednak kvadratu na DN, pa je stoga i preostali kvadrat na KQ jednak kvadratu na NM. Prema tome je QK jednako MN. I pošto su dve duži QA i AK jednake dvema dužima MD i DN, svaka svakoj, i osnovica QK jednaka osnovici MN, biće i ugao QAK jednak uglu MDN [I.8].
Na ovaj način, ako su data dva jednaka ravna ugla i tako dalje kako je u tekstu teoreme. [A to je trebalo dokazati].