25.
Ako je paralelepiped presečen sa ravni paralelnom njegovim suprotnim paralelnim ravnima, odnosiće se osnova prema osnovi kao telo prema telu.
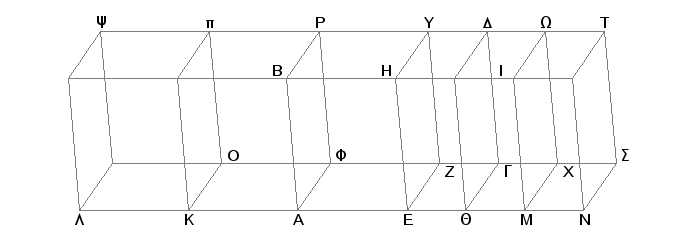
Zaista, neka je paralelepiped ABGD presečen sa ravni ZH, paralelnom suprotnim ravnima PA i DQ. Tvrdim da je osnova AEZF prema osnovi AQGZ kao telo ABZY prema telu EHGD.
Zaista, produžimo AQ na obe strane i odmerimo, koliko želimo, duži AK, KL jednake AE, duži QM, MN jednake EQ i dopunimo paralelograme LO, KF, QX, MS i tela Lp, KP, DM i MT. Pošto su duži LK, KA, AE jednake među sobom, biće jednaki među sobom i paralelogrami KX, KB, AH, a isto tako i paralelogrami LY, Kp, AP jednaki među sobom, jer su naspramni [XI.24]. Iz istih razloga su paralelogrami EG, QX, MS jednaki među sobom, i paralelogrami QH, QI i IN jednaki među sobom, a takođe i DQ, MS, NT; znači tri ravni Lp, KP i AY tela jednake su trima ravnima. Ali ove tri jednake su trima naspramnim. Prema tome su i tri tela Lp, KP i AY jednaka među sobom. Iz istih razloga su i tri tela ED, DM i MT jednaka među sobom. Prema tome koliki je osnova LZ multiplum osnove AZ, toliki je i telo LY multiplum tela AY. Iz istih razloga koliki je osnova NZ multiplum osnove ZQ, toliki je multiplum i telo NY tela QY. Te ako je osnova LZ jednaka osnovi NZ, biće i telo LY jednako telu NY; ako je osnova LZ veća od osnove NZ, biće i telo LY veće od tela NY, a ako je manja, biće manje. Dakle, od četiri uočene veličine, dve osnove AZ i ZQ, i dva tela AY i YQ, uzeti su jednaki multiplumi osnove AZ i tela AY, i to osnova LZ i telo LY, a od osnove QZ i od tela QY osnova NZ i telo NY, i dokazano je da će, ako je osnova LZ veća od osnove ZN, biti i telo LY veće od tela NY; ako je jednaka, biće jednako, a ako je manja, biće manje.
Na ovaj način je osnova AZ prema osnovi ZQ kao telo AY prema telu YQ [V, Def. 5]. A to je trebalo dokazati.