24.

Ako je telo obuhvaćeno paralelnim ravnima, naspramne ravni su jednaki paralelogrami.

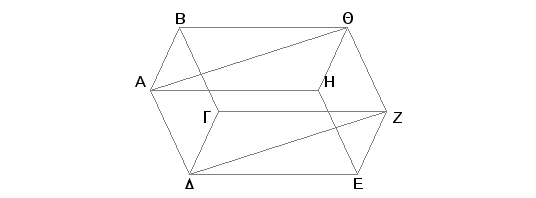
Zaista, neka je telo GDQH obuhvaćeno paralelnim ravnima AG, HZ, DZ, BZ, AE. Tvrdim da su naspramne ravni jednaki paralelogrami.
Zaista, pošto su dve paralelne ravni BH i GE presečene sa ravni AG, njihovi zajednički preseci paralelni su [XI.16]. Prema tome je AB paralelno sa DG. Dalje, pošto su dve paralelne ravni BZ i AE presečene sa ravni AG, njihovi zajednički preseci su paralelni [XI.16]. Prema tome je BG, paralelno sa AD. A dokazano je da je i AB paralelno sa DG. Prema tome je AG paralelogram. Na sličan način se dokazuje da je i svaki od DZ, ZH, HB, BZ, AE paralelogram.
Spojimo AQ, DZ. Pošto je AB paralelno sa DG, a BQ sa GZ, imamo dve duži AB, BQ koje se seku, paralelne sa dvema dužima DG i GZ, koje se seku, no ne u istoj ravni. One čine jednake uglove [XI.10]. Prema tome je ugao ABQ jednak uglu DGZ. I pošto su dve duži, AB i BQ jednake dvema dužima DG i GZ [I.34], i ugao ABQ jednak uglu DGZ, biće i osnovica AQ jednaka osnovici DZ, i trougao ABQ jednak trouglu DGZ [I.4]. I udvostručeni trougao ABQ je paralelogram BH, a udvostručeni trougao DGZ je paralelogram GE [I.34]. Prema tome je paralelogram BH jednak paralelogramu GE. Na sličan način se dokazuje da je paralelogram AG jednak paralelogramu HZ, a i AE paralelogramu BZ.
Na ovaj način, ako je telo obuhvaćeno paralelnim ravnima, naspramne ravni su jednaki paralelogrami. A to je trebalo dokazati.