16.
Ako se dve paralelne ravni preseku nekom ravni, njihovi zajednički preseci paralelni su.
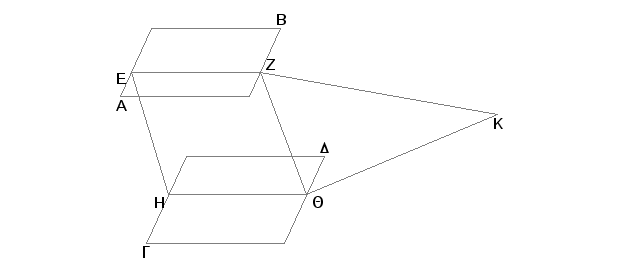
Zaista, neka su dve paralelne ravni AB i GD presečene sa ravni EZHQ i EZ i HQ njihovi zajednički preseci. Tvrdim, da je prava EZ paralelna sa pravom HQ. Zaista, ako to nije tako, onda se EZ i HQ susreću, bilo sa strane ZQ, bilo sa strane EH. Produžimo ih sa strane Z i Q i neka se susreću prvo u tački K. Pošto se EZK nalazi u ravni AB, nalaze se sve tačke EZK u ravni AB [XI.1]. A kako tačka K pripada pravoj EZK, i ona se nalazi u ravni AB. Iz istih razloga zaključujemo da se tačka K nalazi u ravni GD. Na ovaj način se ravni AB i GD, produžene, susreću. Ali one se ne susreću, jer su, po pretpostavci paralelne. Prema tome prave EZ i HQ, produžene sa strane Z i Q, ne susreću se. Na sličan način se dokazuje da se prave EZ i HQ ne susreću produžene ni sa strane E i H. A one koje se ne susreću ni sa jedne strane, paralelne su [I, Def. 23]. Prema tome EZ je paralelno sa HQ.
Na ovaj način, ako se dve paralelne ravni preseku nekom ravni, njihovi zajednički preseci paralelni su. A to je trebalo dokazati.