15.
Ako su dve prave, koje se seku, paralelne dvema drugim pravima, koje se seku, a ne nalaze se u istoj ravni, njihove ravni su paralelne.
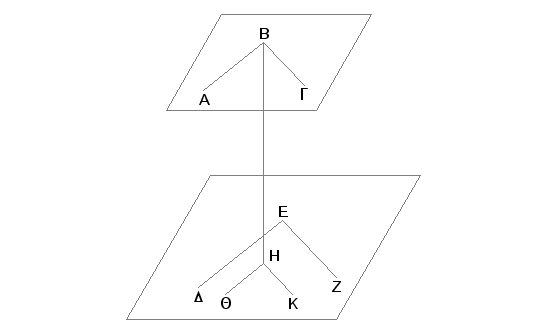
Zaista, neka su dve prave AB i BG, koje se seku paralelne pravima DE i EZ, ali ravan prvih pravih je različita od ravni drugih. Tvrdim da ravni koje prolaze kroz AB, BG i kroz DE, EZ i produžene ne susreću jedna drugu.
Zaista, povucimo kroz tačku B normalu BH na ravan pravih DE i EZ i neka ona prodire tu ravan u tački H, pa povucimo i kroz H pravu HQ paralelno ED i pravu HK paralelno EZ [I.31]. Pošto je prava BH upravna na ravni pravih DE i EZ, biće ona upravna i na svakoj pravoj u toj ravni koja je seče. Prema tome je ona upravna i na pravima HQ i HK, koje se nalaze u ravni pravih DE i EZ [XI, Def. 3]. Znači svaki od uglova BHQ i BHK je prav. I pošto je BA paralelna HQ [XI.9], biće zbir uglova HBA i BHQ jednak sa dva prava ugla [I.29]. No ugao BHQ je prav, pa prema tome mora biti i ugao HBA prav. Dakle, HB je pod pravim uglom prema BA. Iz istih razloga je HB pod pravim uglom i prema BG. I pošto sad prava HB stoji upravno na dvema pravima, koje se seku, BA i BG, biće HB normala na ravni pravih BA i BG. Iz istih razloga BH je normala i na ravni pravih HQ i HK. A ravan tih pravih je isto što i ravan pravih DE i EZ. Prema tome je BH normala i na ravni pravih DE i EZ. A BH je normala i na ravni pravih AB i BG [XI.4]. No ravni, upravne na istoj pravoj, paralelne su [XI.14]. Prema tome je ravan pravih AB i BG paralelna sa ravni pravih DE i EZ.
Na ovaj način, ako su dve prave, koje se seku, paralelne dvema drugim pravima, koje se seku, a ne nalaze se u istoj ravni, njihove ravni su paralelne. A to je trebalo dokazati.