14.
Ravni upravne na istoj pravoj paralelne su.
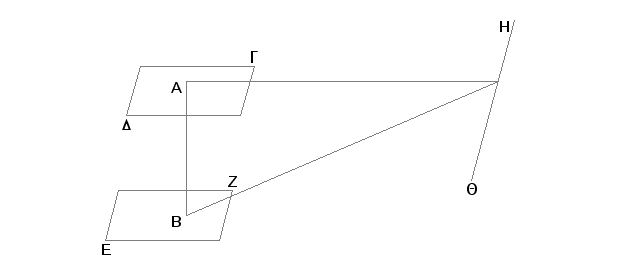
Zaista, neka je prava AB upravna na svakoj od ravni GD i EZ. Tvrdim da su te ravni paralelne.
Zaista, ako to nije tako, one se produžene susreću. Neka se susreću; tada postoji zajednički presek - prava linija [XI.3]. Neka to bude prava HQ. Uzmimo na HQ proizvoljnu tačku K i spojimo AK i BK. Pošto je AB normala na ravni EZ, biće AB normala i na BK, pošto se BK nalazi u ravni EZ upravnoj na AB [XI, Def. 3]. Prema tome je ugao ABK prav. Iz istih razloga je i ugao BAK prav. Na ovaj način trougao ABK ima dva prava ugla - ABK i BAK. A to je nemoguće [I.17]. Prema tome ravni GD i EZ i produžene ne susreću se [XI, Def. 8]. Znači ravni GD i EZ su paralelne.
Na ovaj način, ravni upravne na istoj pravoj paralelne su. A to je trebalo dokazati.