11.
Iz date tačke van ravni povući pravu upravnu na tu ravan.
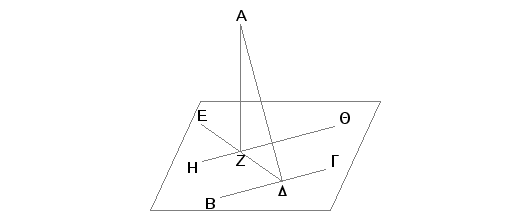
Neka je A data tačka nad datom osnovnom ravni. Treba iz date tačke A povući pravu liniju upravnu na datu osnovnu ravan.
Povucimo u osnovnoj ravni proizvoljnu pravu BG i konstruišimo iz tačke A normalu AD upravnu na BG [I.12]. Ako je AD normala na osnovnoj ravni, traženo je postignuto. Ako nije, povucimo u osnovnoj ravni iz tačke D normalu DE na pravu BG [I.11] i spustimo iz tačke A normalu AZ na pravu DE [I.12], pa kroz tačku Z povucimo pravu HQ paralelnu pravoj BG [I.31].
Pošto je BG upravna na svakoj od DA i DE, biće BG upravna i na ravni EDA [XI.4]. No njoj je paralelna i prava HQ. A ako su dve prave paralelne i jedna od njih upravna na nekoj ravni, onda je i druga upravna na toj ravni [XI.8]. Prema tome je HQ upravna na ravni pravih ED i DA koja seče pravu HQ. No nju seče prava AZ, koja se nalazi u ravni pravih ED i DA [XI, Def. 3]. Prema tome je HQ upravna na ZA. A znači i ZA je upravna na QH. No AZ je upravna i na DE. AZ je na taj način upravna na svakoj od HQ i DE. Ali ako je kroz tačku preseka dve prave povučena prava normalna na tim pravima biće povučena prava normalna i na ravan tih pravih [XI.4]. Prema tome je ZA upravna na ravan pravih ED i HQ. No ravan pravih ED i HQ je osnovna ravan. Prema tome je ZA prava upravna na osnovnoj ravni.
Na ovaj način je iz date tačke A van ravni povučena prava AZ upravna na datoj ravni. A to je trebalo izvesti.