10.
Ako su dve prave, koje se seku, paralelne sa dvema pravima, koje se seku, no ne nalaze se sa ovima u istoj ravni, one obrazuju jednake uglove.
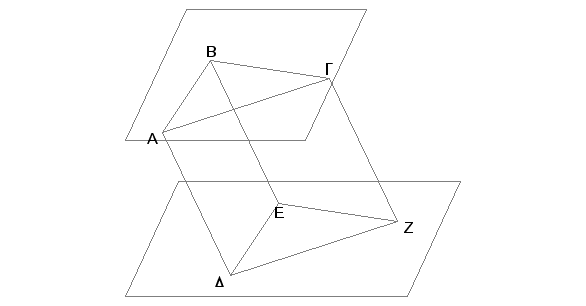
Zaista, neka su AB i BG dve prave, koje jedna drugu seku, paralelne sa pravima DE i EZ, koje seku jedna drugu, no ne nalaze se u istoj ravni sa prvim pravima. Tvrdim, da je ugao ABG jednak uglu DEZ.
Zaista, odmerimo duži BA, BG, ED, EZ jednake među sobom i spojimo AD, GZ, BE, AG, DZ. Pošto je BA jednako i paralelno ED, biće i AD jednako i paralelno BE [I.33]. Iz istih razloga je i GZ jednako i paralelno BE. Prema tome je svaka od AD i GZ jednaka i paralelna sa BE. No prave koje su paralelne istoj pravoj, a ne nalaze se sa njom u istoj ravni paralelne su [XI.9]. Prema tome je AD paralelna GZ i jednaka. A spajaju ih AG i DZ pa je znači i AG jednaka DZ i paralelna [I.33]. I pošto su dve strane AB i BG jednake dvema stranama DE i EZ i osnovica AG jednaka osnovici DZ, biće ugao ABG jednak uglu DEZ [I.8].
Na ovaj način, ako su dve prave, koje se seku, paralelne sa dvema pravima, koje se seku, no ne nalaze se sa njima u istoj ravni, one obrazuju jednake uglove. A to je trebalo dokazati.