8.
U dati kvadrat upisati krug.
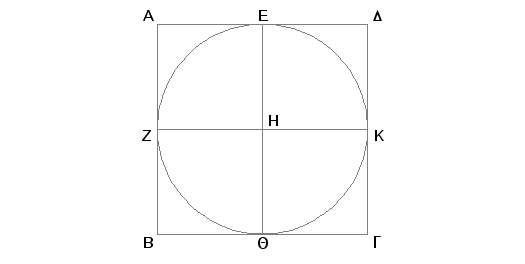
Neka je dat kvadrat ABGD, treba u kvadrat ABGD upisati krug.
Prepolovimo svaku od pravih AD i AB tačkama E i Z i kroz tačku E povucimo pravu EQ paralelnu svakoj od pravih AB i DG, a kroz tačku Z pravu ZK paralelnu svakoj od pravih AD i BG. Tada je svaka od slika AK, KB, AQ, QD, AH, HG, BH, HD paralelogram i njihove suprotne strane, očevidno, su jednake [I.34]. Kako je AD jednako AB i AE polovina od AD, a AZ polovina od AB, biće i AE jednako AZ, a kako su jednake i njima suprotne strane, biće i ZH jednako HE. Na sličan način se dokazuje da je svaka od HQ i HK jednaka svakoj od ZH i HE. Prema tome su četiri prave HE, HZ, HQ, HK međusobno jednake. Zbog toga će krug nacrtan sa centrom u H jednim od rastojanja do tačaka E, Z, Q, K proći i kroz ostale tačke i dodirnuti prave AB, BG, GD, DA, jer su uglovi kod tačaka E, Z, Q, K pravi. Zaista, kad bi krug sekao prave AB, BG, GD, DA, tangenta kruga na kraju prečnika bila bi u krugu, a dokazano je da je to besmisleno [III.16]. Prema tome krug opisan sa centrom u H sa jednim od rastojanja do tačaka E, Z, Q, K ne seče prave AB, BG, GD, DA. Znači on ih dodiruje i upisan je u kvadrat ABGD.
Na ovaj način je u dati kvadrat upisan krug. A to je trebalo izvesti.