7.
Oko datog kruga opisati kvadrat.
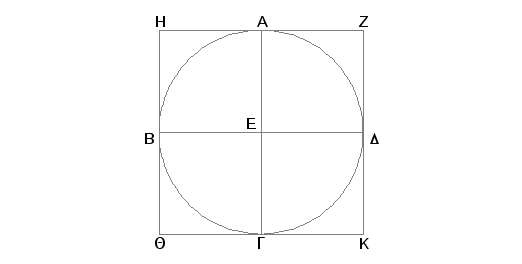
Neka je dat krug ABGD. Treba oko kruga ABGD opisati kvadrat.
Povucimo u krugu ABGD dva prečnika AG i BD pod pravim uglovima, i kroz tačke A, B, G, D povucimo prave ZH, HQ, QK, KZ, tangente na krug ABGD [III.16, Posledica].
Pošto je prava ZH tangenta na krug ABGD, a prava EA povučena iz centra E ka tački dodira A, uglovi kod tačke A su pravi [III.18]. Iz istih razloga su uglovi i kod tačaka B, G, D pravi. Kako je ugao AEB prav, a prav i ugao EBH, biće prava HQ paralelna pravoj AG [I.28]. Iz istih razloga je i prava AG paralelna pravoj ZK. Stoga je prava HQ paralelna pravoj ZK [I.30]. Na sličan način se dokazuje da je svaka od pravih HZ i QK paralelna pravoj BED. Prema tome su HK, HG, AK, ZB, BK paralelogrami, što znači da je HZ jednako QK, a HQ jednako ZK [I.34]. A kako je AG jednako BD, a i AG jednako i HQ i ZK, i BD jednako i HZ i QK (pa prema tome je i svaka od HQ i ZK jednaka svakoj od HZ i QK) [I.34], četvorougao ZHQK je jednakostran. A tvrdim da je on i pravougli. Zaista, pošto je HBEA paralelogram, a ugao AEB prav, biće prav i ugao AHB [I.34]. Na sličan način se dokazuje da su uglovi i kod tačaka Q, K, Z pravi. Prema tome je ZHQK pravougaonik, a dokazano je i da je on jednakostran, znači da je on kvadrat, a opisan je oko kruga ABGD.
Na ovaj način, oko datog kruga je opisan kvadrat. A to je trebalo izvesti.