6.
U dati krug upisati kvadrat.
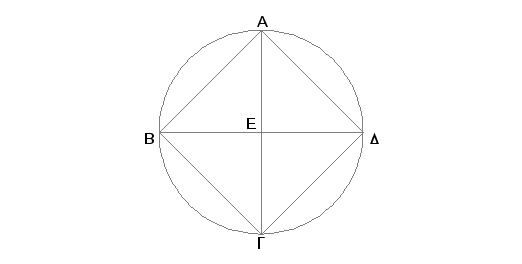
Neka je dat krug ABGD; treba u krug ABGD upisati kvadrat.
Povucimo u krugu ABGD dva prečnika AG, BD upravna jedan na drugi i spojimo AB, BG, GD, DA.
Kako je BE jednako ED, jer je E centar, a EA je zajedničko i pod pravim uglovima, biće osnovica AB jednaka osnovici AD [I.4]. Iz istih razloga je i svaka od BG i GD jednaka svakoj od AB, AD. Prema tome je četvorougao ABGD jednakostran. Tvrdim da je i pravougaonik. Zaista, pošto je prava BD prečnik kruga ABGD, BAD je polukrug. Prema tome je ugao BAD prav [III.31]. Iz istih razloga je svaki od uglova ABG, BGD, GDA prav. Zbog toga je četvorougao ABGD pravougaonik. A dokazano je da je on i jednakostran. Prema tome on je kvadrat [I. Def. 22], a upisan je u krug ABGD.
Na ovaj način je u dati krug upisan kvadrat ABGD. A to je trebalo izvesti.