3.
Oko datog kruga opisati trougao sa uglovima jednakim uglovima datog trougla.
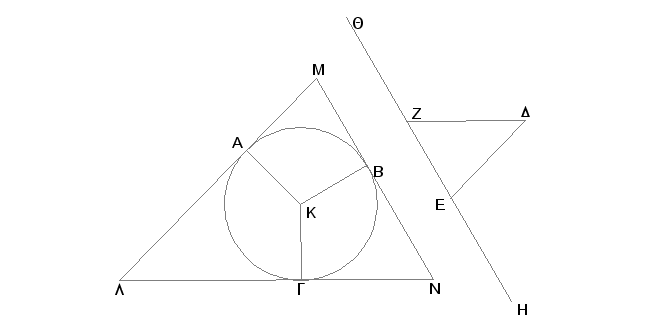
Neka je ABG dati krug i DEZ dati trougao; treba oko kruga ABG opisati trougao sa uglovima jednakim uglovima trougla DEZ.
Produžimo EZ sa obe strane ka tačkama H i Q i uzmimo centar K kruga ABG [III.1]. Povucimo proizvoljno pravu KB i konstruišimo na toj pravoj KB kod tačke K ugao BKA jednak uglu DEH, ugao BKG jednak uglu DZQ [I.23], i kroz tačke A, B, G povucimo na krug ABG tangente LAM, MBN, NGL [III.16, Posledica].
Kako prave LM, MN, NA dodiruju krug ABG u tačkama A, B, G, a prave, što spajaju centar K sa tačkama A, B, G, su KA, KB, KG, uglovi kod tačaka A, B, G su pravi [III.18]. Kako je sad u četvorouglu AMBK zbir četiri ugla jednak četvorostrukom pravom uglu, jer se četvorougao sastoji iz dva trougla, a dva ugla KAM i KBM su prava, onda je i zbir dvaju ostalih uglova AKB i AMB jednak dvostrukom pravom uglu. A zbir uglova DEH i DEZ jednak je dvostrukom pravom uglu [I.13]. Prema tome je zbir uglova AKB i AMB jednak zbiru uglova DEH i DEZ, no kako je ugao AKB jednak uglu DEH, i preostali ugao AMB jednak preostalom uglu DEZ. Na sličan način se dokazuje da je ugao LNB jednak uglu DZE, pa je i preostali ugao MLN jednak preostalom uglu EDZ [I.32]. Znači trougao LMN ima uglove jednake uglovima trougla DEZ, a pri tome je opisan oko kruga ABG.
Na ovaj način, oko datog kruga opisan je trougao sa uglovima jednakim uglovima datog trougla. A to je trebalo izvesti.