15.
U dati krug upisati šestougao sa jednakim stranama i jednakim uglovima.
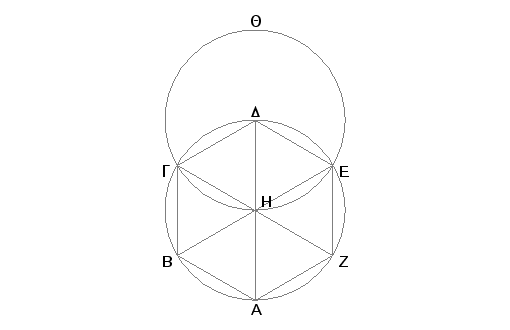
Neka je dat krug ABGDEZ. Treba u krug ABGDEZ upisati šestougao sa jednakim stranama i jednakim uglovima.
Povucimo u krugu ABGDEZ prečnik AD i uzmimo tačku H, centar kruga, i nacrtajmo krug EHGQ sa centrom u D sa rastojanjem (poluprečnikom) DH, pa prave što spajaju E i H odnosno G i H, produžimo do tačaka B i Z i spojimo AB, BG, GD, DE, EZ, ZA. Tvrdim da je šestougao ABGDEZ sa jednakim stranama i jednakim uglovima.
Kako je tačka H centar kruga ABGDEZ, HE jednako je HD. A kako je tačka D centar kruga HGQ, DE jednako je DH. A dokazano je već da je HE jednako HD. Prema tome je i HE jednako ED. Znači trougao EHD je ravnostran, a to znači da su mu sva tri ugla EHD, HDE, DEH međusobno jednaki, jer su uglovi na osnovici ravnokrakog trougla međusobno jednaki [I.5]. A kako je zbir tri ugla u trouglu jednak dvama pravim uglovima [I.32], biće ugao EHD jednak dvema trećinama pravog ugla. Na sličan način se dokazuje da je i ugao DHG jednak dvema trećinama pravog ugla. A kako prava GH stoji prema pravoj EB tako da obrazuje dva susedna ugla EHG i GHB čiji je zbir jednak dvema pravim uglovima, biće i preostali ugao GHB jednak dvema trećinama pravog ugla. Prema tome su tri ugla EHD, DHG, GHB međusobno jednaki, pa su jednaki i unakrsni uglovi BHA, AHZ, ZHE (uglovima EHD, DHG, GHB) [I.15]. Prema tome su šest uglova EHD, DHG, GHB, BHA, AHZ, ZHE međusobno jednaki. A jednaki uglovi se oslanjaju na jednake lukove [III.26], pa zbog toga su i šest lukova AB, BG, GD, DE, EZ, ZA međusobno jednaki. Međutim jednake lukove stežu jednake prave (tetive) [III.29], i prema tome su i tih šest pravih međusobno jednake. Šestougao ABGDEZ je prema tome sa jednakim stranama. Tvrdim da je on i sa jednakim uglovima. Zaista, kako je luk ZA jednak luku ED, dodajmo mu zajednički luk ABGD, tada je ceo luk ZABGD jednak luku EDGBA, a kako se na luk ZABGD oslanja ugao ZED, i na luk EDGBA ugao AZE, biće ugao AZE jednak uglu DEZ [III.27]. Na sličan način se dokazuje, da su i ostali uglovi šestougla ABGDEZ posebice jednaki svakom od uglova AZE, ZED. Prema tome je šestougao ABGDEZ sa jednakim uglovima. A dokazano je da je on i sa jednakim stranama, i upisan u krug ABGDEZ.
Na ovaj način je u dati krug upisan šestougao sa jednakim stranama i jednakim uglovima. A to je trebalo izvesti.